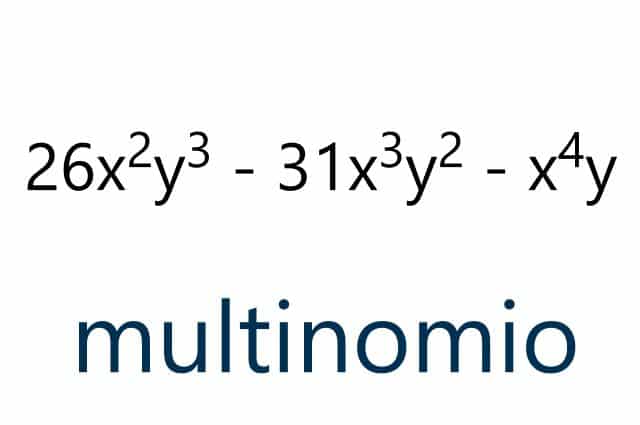
Ejemplo de un multinomio
La noción de multinomio se utiliza en el terreno del álgebra para hacer referencia a una expresión que contiene dos o más términos. Para comprender su significado, por lo tanto, primero hay que saber qué es el álgebra y cuáles son sus expresiones.
 Temas
TemasÁlgebra y aritmética
Se llama álgebra a la rama de las matemáticas dedicada al estudio de estructuras abstractas. En estas estructuras, se recurre a signos, letras y números para la generalización de operaciones aritméticas.
Mientras que la aritmética gira en torno a los números y a las operaciones fundamentales, el álgebra añade las letras para desarrollar la representación de incógnitas (que son cantidades que se desconocen) y parámetros (que pueden ser coeficientes o variables). En este marco, las expresiones que se forman reciben el nombre de fórmulas algebraicas.
El multinomio
Retomando la idea de multinomio, se trata de una cantidad que se expresa mediante dos o más términos en una misma fórmula. Un término algebraico, en tanto, es un producto de factores que aparece representado por letras y números.
Cuando la totalidad de los términos son enteros y racionales y están unidos por los signos menos ( – ) o más ( + ), el multinomio recibe la denominación de polinomio. Por eso puede decirse que un polinomio es un tipo específico de multinomio.
También podemos diferenciar estos dos conceptos teniendo en cuenta que los términos del polinomio deben dar como resultado números naturales o cero, mientras que en los multinomios, las variables pueden encontrarse en radicales. Esto no indica necesariamente que la complejidad del multinomio siempre sea mayor que la del polinomio, pero suele ser así por su mayor amplitud en cuanto a los tipos de valores que admite.
Es importante diferenciar entre los multinomios, los monomios y los binomios. Mientras que los multinomios cuentan con varios términos, los monomios sólo presentan un único término. Un binomio, por otro lado, es una expresión que consta de dos términos algebraicos relacionados por los signos menos o más.
Teorema multinomial
En el ámbito de las matemáticas existe un concepto relacionado con los multinomios que se conoce con el nombre de teorema multinomial. Se trata de la expansión de la potencia de una suma, de manera que se pueda expresar como las potencias de sus términos. Su base se encuentra en el teorema del binomio, el cual en este caso se encuentra generalizado para su uso en polinomios o multinomios.

El teorema multinomial es una generalización del teorema del binomio.
Con respecto a este último teorema, es una fórmula que permite desarrollar la enésima potencia de cualquier binomio, siempre que la cantidad (que se representa con la variable n) pertenezca al conjunto de los números enteros positivos, es decir que no incluye las fracciones ni los números decimales. Lo que propone es la expansión de la potencia (x + y)n en la siguiente suma de términos axbyc, siendo los exponentes b y c números naturales cuya suma sea igual a n. Por lo general, si un exponente es cero se omite la potencia a la que afecta, ya que su resultado es 1 y no altera el resultado del binomio, multinomio o polinomio.
Volviendo al teorema multinomial específicamente, si tenemos un entero positivo y uno que no sea negativo, a los cuales podemos adjudicarles las variables m y n, respectivamente, gracias a esta fórmula podemos observar la expansión de la suma de m términos cuando elevamos todo a la potencia n. Así como en el caso del binomio, si el exponente es cero se suele dejar fuera la potencia, también si la base es igual a cero. Por último, dado que este teorema está basado en el del binomio, si la cantidad de términos es igual a dos, se aplica éste.

