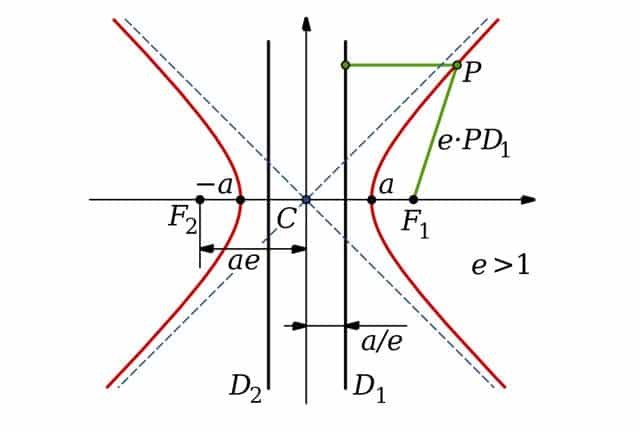
La hipérbola es una curva con dos focos y simétrica a dos ejes perpendiculares entre sí.
El vocablo griego hyperbolḗ llegó al latín como hyperbŏla. A nuestro idioma el concepto arribó como hipérbola, un término que se emplea en el terreno de la geometría.
 Temas
TemasCurva
Se denomina hipérbola a la curva con dos focos que resulta simétrica respecto a un par de ejes perpendiculares entre sí. Para trazar una hipérbola, se corta un cono recto con un plano, generando un ángulo menor que aquel que forma la generatriz respecto al eje de revolución.
Una hipérbola presenta dos ramas abiertas. Ambas se dirigen en sentidos opuestos, aproximándose de forma indefinida a dos asíntotas. Esto hace que, considerando dos puntos fijos, la diferencia de sus distancias sea constante.
De acuerdo a la menor o mayor abertura de las ramas de la hipérbola, se calcula su excentricidad. Esta excentricidad se conoce dividiendo la mitad de la distancia del eje focal por la mitad de la distancia del eje mayor.
Su ecuación general es Ax2 – Cy2 + Dx + Ey + F = 0. Nótese que en las ecuaciones matemáticas debemos interpretar partes como Ax o Ey como la multiplicación de las dos variables. Si A y C son mayores de 0 y sus coeficientes tienen signos opuestos, entonces estamos ante la representación de una hipérbola con ejes paralelos a los coordenados.
Elementos de la hipérbola
Una definición formal indica que considerados dos puntos (F1 y F2) que se denominan focos, la hipérbola es el conjunto de los puntos del plano en los cuales el valor absoluto que se registra al considerar la diferencia de sus distancias a los focos (los mencionados F1 y F2) es constante.
Además de los focos, en la hipérbola es posible reconocer otros elementos. Entre ellos aparecen el eje focal (la recta que pasa por ambos focos), el eje secundario (la mediatriz que une el segmento que va de un foco a otro), el centro (el punto de intersección de estos ejes) y los vértices.
Conceptos relacionados
A continuación veremos una breve definición de algunos de los conceptos complementarios antes mencionados. Comencemos por asíntota, el nombre que recibe una recta a la cual se acerca de forma continua la gráfica de una función dada; dicho de otra manera, la distancia entre ambas tiende a cero, aunque se extienden de manera indefinida. También se puede decir que su comportamiento es asintótico. Un ejemplo de esto se puede observar en las funciones racionales.
También hemos hablado de generatriz, una línea que por su movimiento se aprecia como una figura geométrica. Puede ser una línea curva (que genere elipsoides, esferas, etcétera) o una recta (que gire con respecto a un eje de rotación para formar superficies cilíndricas o cónica, entre otras). Uno de los conceptos más importantes en este contexto es el de foco, el cual pertenece al ámbito de la geometría y se puede vincular a una superficie o una curva. Se trata de un punto que no suele pertenecer a éstos, aunque sí permite mantener ciertas distancias constantes con todos sus puntos.
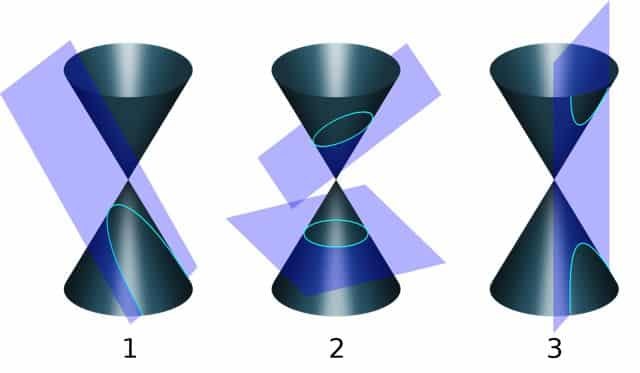
En el tercer tipo de sección cónica podemos apreciar una hipérbola.
Primeros usos en la historia
El descubrimiento de las secciones cónicas estuvo a cargo de Menecmo, nacido en Grecia en el año 380 a. C. y especializado en las matemáticas y la geometría. El contexto de tal hito fue su investigación acerca de la duplicación del cubo, un problema que lo llevó a demostrar que se podía solucionar cortando una parábola con una hipérbola, algo que más adelante confirmaron Proclo y Eratóstenes.
Si bien Menecmo usó la hipérbola en su trabajo, pasó alrededor de un siglo hasta que alguien acuñara este término. Y fue el matemático y astrónomo griego Apolonio de Perge, quien lo incluyó en su tratado titulado Cónicas, uno de los escritos más importantes de la época.

