Antes de entrar de lleno en el significado del término logaritmo natural que ahora nos ocupa, vamos a proceder a descubrir el origen etimológico de las dos palabras que le dan forma:
-Logaritmo, en primer lugar, deriva del griego. Buena muestra de eso es que el resultado de la suma de dos componentes léxicos de dicha lengua: “logos”, que significa “palabra”, y “arithmós”, que puede traducirse como “número relativo”. Se trata de un término que fue utilizado por primera vez por el matemático de origen escocés John Napier (1550 – 1617). Él fue el pionero, por tanto, en definir los logaritmos.
-Natural, en segundo lugar, procede del latín. Exactamente emana de “naturalis”, que significa “relativo a la naturaleza” y que se forma a partir de la unión de estos componentes léxicos: el adjetivo “natum”, que equivale a “nacido”; el sufijo “-ura”, que se usa para indicar el resultado de la acción, y el sufijo “-al”, que significa “relativo a”.
Se denomina logaritmo al número al cual se debe elevar una cantidad positiva para que el resultado sea una cierta cifra. La función logaritmo, por lo tanto, le asigna un exponente (una potencia) a un número (llamado argumento), al cual la base (otro número) tiene que elevarse para obtenerlo.
Esto quiere decir que la base elevada a la potencia debe dar como resultado el argumento. El logaritmo en base 3 de 81 es 4, ya que 81 (el argumento) es igual a 3 (la base) elevado a la potencia 4.
Base a la potencia = Argumento
3 elevado a la 4 = 81
3 x 3 x 3 x 3 = 81
De acuerdo a sus características, existen diferentes tipos de logaritmos. El logaritmo natural, también llamado logaritmo neperiano, es aquel que cuenta con el número e como base.
Como se puede advertir, para comprender qué es un logaritmo natural resulta indispensable entender el concepto de número e. Así se llama a una constante matemática que equivale a 2,718281828459…
Este número e es la base de los logaritmos naturales. Se trata de un número trascendente (es decir, no algebraico) e irracional (su expresión decimal no es periódica ni tampoco exacta).
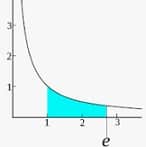
Puede decirse, por lo tanto, que el logaritmo natural de un número x es el exponente al cual tiene que elevarse el número e para obtener como resultado x. El matemático Nikolaus Mercator (1620-1687) es señalado como la primera persona que mencionó la idea de logaritmo natural en una publicación, aunque en un principio se le dio el nombre formal de logaritmo hiperbólico ya que sus valores eran correspondientes a los del sector ubicado debajo de la hipérbola.
Además de todo lo indicado, tenemos que exponer que el logaritmo natural tiene distintas aplicaciones. No obstante, entre las más significativas podemos destacar las siguientes:
-Para calcular lo que es la decadencia radiactiva.
-Es muy utilizado en el ámbito de la estadística para proceder a transformar los datos. Una transformación que puede ser necesaria por distintas razones.
-Para calcular las funciones de densidad de probabilidad.
-Se puede emplear para trabajar con lo que es el crecimiento exponencial en las llamadas poblaciones biológicas.
