
Pitágoras de Samos fue un importante matemático y filósofo de la Antigüedad.
Se conoce como teorema a la proposición que puede ser demostrada de manera lógica a partir de un axioma o de otros teoremas que ya hayan sido respectivamente demostrados. En este contexto es fundamental respetar algunas reglas de inferencia para arribar a dicha demostración.
Pitágoras de Samos (582 a.C.–507 a.C.), asimismo, fue un filósofo y matemático de origen griego. A diferencia de lo que puede llegar a suponerse, Pitágoras no fue quien creó el teorema que lleva su nombre. Dicho teorema fue desarrollado y aplicado mucho tiempo antes en Babilonia y la India; sin embargo, la escuela pitagórica (y no el propio Pitágoras) fue pionera en hallar una demostración formal para este teorema.
Pitágoras podemos decir además que está considerado como el primer matemático puro de toda la historia y ayudó de manera sólida al desarrollo de áreas científicas como es el caso de las citadas matemáticas pero también de la geometría, la aritmética, la astronomía y la música. Y todo gracias tanto a su citado teorema como a otros importantes descubrimientos como la significación funcional de los números o la inconmensurabilidad de los lados y de la diagonal de lo que es el cuadrado.
 Temas
TemasQué es el teorema de Pitágoras
En concreto, se puede afirmar que el denominado teorema de Pitágoras señala que el cuadrado de la hipotenusa, en los triángulos rectángulos, es igual a la suma de los cuadrados de los catetos. Para comprender esta sentencia, hay que tener en cuenta que un triángulo que se identifica como rectángulo es aquel que posee un ángulo recto (es decir, que mide 90º), que la hipotenusa consiste en el lado de más longitud de dicha figura (y opuesto al ángulo recto) y que los catetos se caracterizan por ser los dos lados menores del triángulo recto.
La importancia que tiene, por tanto, este teorema que ahora nos ocupa es que nos permite descubrir una medida en base a dos datos concretos. Es decir, aquel supuso un paso importante dentro del ámbito matemático porque consiguió que conociendo las longitudes de dos lados de un triángulo rectángulo podamos averiguar cual es la longitud del tercer lado.
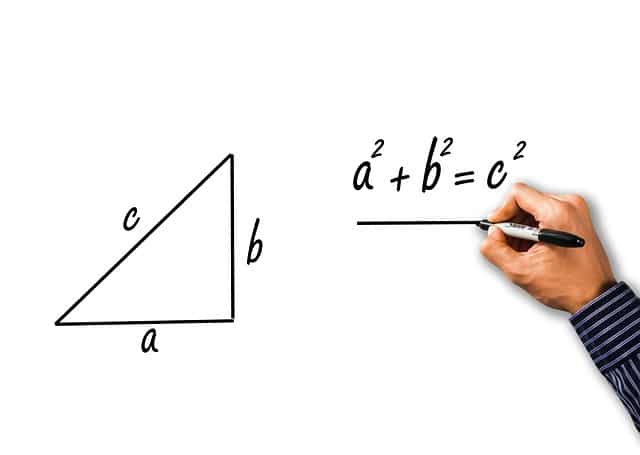
De acuerdo al teorema de Pitágoras, en un triángulo rectángulo, el cuadrado de la hipotenusa es equivalente a la suma de los cuadrados de los catetos.
Las demostraciones
En 1927, el matemático E. S. Loomis recopiló más de 350 demostraciones del teorema de Pitágoras. Loomis clasificó dichas demostraciones en cuatro grupos: las demostraciones geométricas, que se realizan en base a la comparación de áreas; las demostraciones algebraicas, desarrolladas en función del vínculo entre los lados y los segmentos del triángulo; las demostraciones dinámicas, que apelan a las propiedades de fuerza; y las demostraciones cuaterniónicas, que surgen con el uso de vectores.
En el caso de las demostraciones geométricas habría que destacar que muchos son los autores o científicos que a lo largo de la historia las han llevado a cabo. Entre ellos habría que resaltar, por ejemplo, al gran filósofo Platón, que las desarrolló en sus famosos diálogos, o al matemático Euclides.
Las algebraicas también han propiciado que diversos personajes hayan decidido, de un modo u otro, plantearlas, desarrollarlas y demostrarlas de una manera real y palpable. Así, en este caso, habría que citar a figuras tan ilustres como Leonardo da Vinci que ha llevado a cabo la construcción y demostración de esta forma del citado Teorema de Pitágoras.

