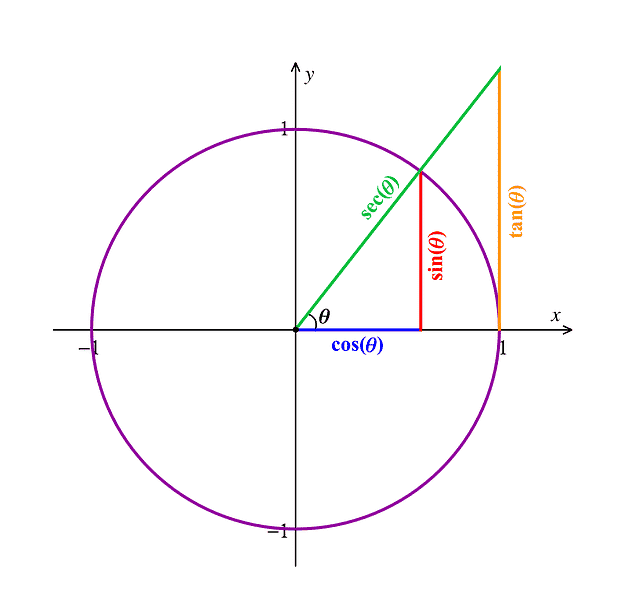
A la función inversa del seno de un ángulo o arco se la denomina cosecante.
Cosecante es la función inversa del seno de un arco o de un ángulo. Se trata de un concepto que se emplea en el ámbito de la trigonometría, una rama de las matemáticas vinculada a la geometría.
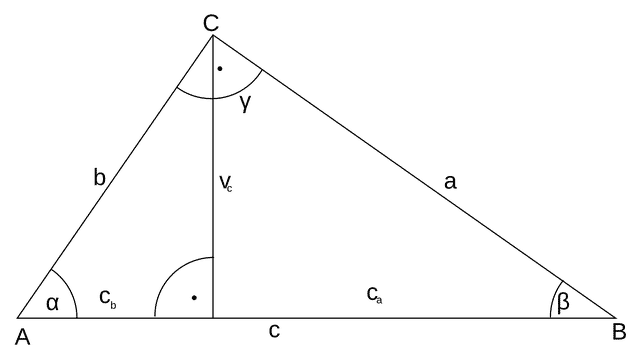
Para comprender qué es la cosecante, primero hay que saber qué es el seno. Esta función, en un triángulo rectángulo, se obtiene dividiendo el cateto opuesto a un ángulo agudo y la hipotenusa. Cabe recordar que la hipotenusa es el lado más extenso de un triángulo rectángulo, mientras que los otros dos lados reciben el nombre de catetos.
Por lo tanto, si el seno es igual al cateto opuesto dividido por la hipotenusa, la cosecante se obtiene dividiendo la hipotenusa por el cateto opuesto ya que se trata de la función inversa. Al mismo resultado se llega obteniendo el cociente de 1 y el seno.
 Temas
TemasEjemplo de cosecante
En un triángulo rectángulo cuya hipotenusa mide 10 centímetros y el cateto opuesto mide 4 centímetros, la cosecante será igual a 2,5:
Cosecante = Hipotenusa / cateto opuesto
Cosecante = 10 / 4
Cosecante = 2,5
Esto se puede comprobar dividiendo 1 y el seno. Si el seno equivale al cateto opuesto dividido la hipotenusa:
Seno = Cateto opuesto / Hipotenusa
Seno = 4 / 10
Seno = 0,4
Y luego:
Cosecante = 1 / Seno
Cosecante = 1 / 0,4
Cosecante = 2,5
La cosecante tiene diversas aplicaciones prácticas.
Su relación con el seno
Cabe destacar que la relación entre la cosecante y el seno es similar a la que mantiene la función coseno con su inversa, la secante, y al vínculo que establecen la función tangente y la cotangente (su inversa).
Dado que todas estas funciones son prácticamente imposibles de resolver mentalmente para la mayoría de las personas, y que en los cálculos cotidianos los valores de los ángulos dados suelen ser más o menos los mismos, es posible elaborar una tabla con la cosecante de los ángulos más comunes, entre los cuales se encuentran el nulo (0°), el de 30°, el de 90° y el de 270°, entre otros.
Uso de la función cosecante
Es importante entender que la cosecante puede parecer demasiado abstracta en comparación con otras partes del mundo de los números si la miramos desde el uso que hace de las matemáticas la mayoría de la gente en su vida cotidiana, pero se trata de una función muy útil que tiene aplicaciones prácticas para resolver diferentes problemas que sí repercuten en nuestro día a día, aunque no lo sepamos.
Por ejemplo, tanto la cosecante como el resto de las funciones expresadas más arriba se usan con mucha asiduidad en el ámbito de la programación informática, para resolver problemas a la hora de desarrollar un videojuego o una película de animación en tres dimensiones. No olvidemos que detrás de las imágenes generadas por ordenador hay millones de figuras geométricas, siendo el triángulo la más importante, y es precisamente esta última que aprovecha especialmente la cosecante para resolver, por ejemplo, los valores de sus lados.
Los triángulos, a su vez, tienen más de una aplicación en el mundo de los gráficos en tres dimensiones: por un lado, son la base de los modelos, es decir, de los personajes y los escenarios, ya que se construyen a partir de ellos, aunque una vez aplicadas varias técnicas de renderizado casi no se note su presencia y las superficies cobren un aspecto «suave»; pero también el triángulo puede servir de guía imaginaria para computar la posición de un punto luego de una determinada traslación, y es ahí donde el uso de la cosecante puede servirnos.
Si tenemos un triángulo rectángulo del cual conocemos uno de sus ángulos y su lado opuesto, podemos comenzar por elaborar la ecuación cosecante del ángulo = hipotenusa / opuesto para averiguar el valor de la hipotenusa, ya que los otros dos los conocemos.

