El término covarianza no forma parte del diccionario elaborado por la Real Academia Española (RAE). El concepto, de todos modos, se utiliza en el ámbito de la estadística y en el de la probabilidad para nombrar al valor que refleja el grado de variación conjunta que se registra en dos variables aleatorias tomando como medida sus medias.
La covarianza, por lo tanto, nos permite descubrir si las variables mantienen un vínculo de dependencia. El dato también contribuye a conocer otros parámetros.
Se conoce con el nombre de variable aleatoria a una función que al resultado de un experimento aleatorio le asigna un valor, por lo general de tipo numérico. Un experimento aleatorio, por otra parte, es el que puede arrojar diferentes resultados aunque se realice más de una vez bajo las mismas condiciones, de manera que cada experiencia se vuelve imposible de predecir y, por lo tanto, de reproducir.
Un ejemplo muy común de experimento aleatorio, que podemos probar en nuestra vida cotidiana, es el lanzamiento de un dado: aunque se arroje sobre la misma superficie, con la misma mano o cubilete, y aplicando más o menos la misma fuerza y dirección, no es posible predecir cuál de sus caras quedará apuntando hacia arriba.
Si los valores bajos de una variable se corresponden con los valores bajos de otra variable, o si lo mismo ocurre con los valores altos de ambas, la covarianza tiene un valor positivo y es calificada como directa. En cambio, si los valores bajos de una variable se corresponden con los valores más altos de otra variable y viceversa, la covarianza resulta negativa y se define como inversa. La tendencia existente en la relación lineal que se establece entre las variables, de este modo, es expresada mediante el signo de la covarianza.
Existen distintas fórmulas para calcular la covarianza. Puede decirse que la covarianza es la media aritmética que surge del producto de las desviaciones de las variables respecto a sus propias medias.
Supongamos que las variables son los resultados de las evaluaciones de Historia y Geografía de cinco estudiantes:
Calificaciones Historia (P) de los cinco alumnos: 6, 5, 7, 7, 4 (total = 29)
Calificaciones Geografía (S) de los cinco alumnos: 7, 3, 4, 3, 5 (total = 22)
Luego hay que tabular, multiplicando los resultados de las evaluaciones de cada alumno:
P x S: 42 (ya que 6 x 7 = 42), 15 (5 x 3), 28 (7 x 4), 21 (7 x 3), 20 (4 x 5). Total de la suma de los resultados = 126)
La media de P: 29 / 5 = 5,8
La media de S: 22 / 5 = 4,4
Finalmente:
Covarianza PS: (126 / 5) – 5,8 x 4,4
Covarianza PS: 25,2 – 5,8 x 4,4
Covarianza PS: 25,2 – 25,52
Covarianza PS: -0,32
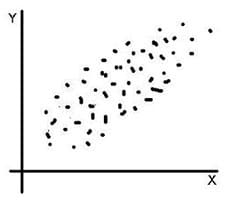Además de saber si dos variables aleatorias dadas tienen un vínculo de dependencia mutuo, la covarianza sirve para la estimación de parámetros tales como la recta de regresión y el coeficiente de correlación lineal.
La recta de regresión también se conoce como ajuste lineal o regresión lineal, y es un concepto perteneciente al ámbito de la estadística que comprende un modelo matemático utilizado para aproximar la dependencia que existe entre un grupo de variables y un término aleatorio.
El coeficiente de correlación lineal, por otro lado, es un indicador de la dirección y la fuerza que posee una relación lineal (en matemáticas, lo que se da si el valor de una magnitud depende del que tiene otra) y una proporcionalidad (una razón o relación constante que ocurre entre magnitudes que puedan ser medidas) entre dos variables estadísticas (son características que pueden fluctuar, con valores que pueden ser observados y medidos).
Es importante diferenciar los siguientes dos tipos de covarianza: la que se da entre dos variables aleatorias, que se considera una propiedad de la distribución conjunta, es decir, de los eventos de ambas que ocurren de manera simultánea; la muestral, que se utiliza a modo de estimación estadística del parámetro.
