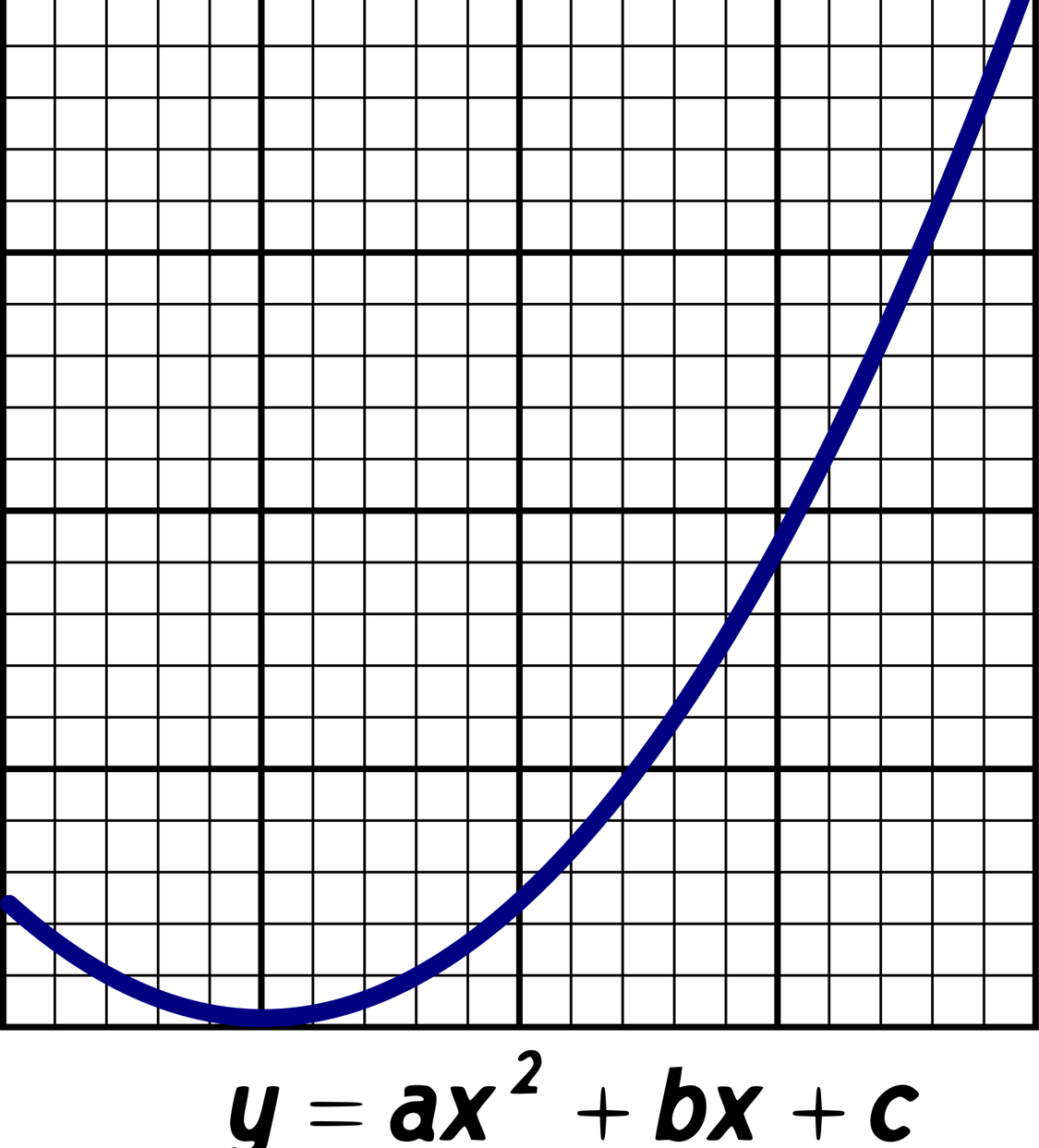
Una función cuadrática es un polinomio de segundo grado.
Una función cuadrática es una función matemática que se puede expresar como una ecuación con la siguiente forma: f (x) = ax al cuadrado + bx + c.
En este caso, a, b y c son los términos de la ecuación: números reales, con a siempre con valor diferente a 0. Debe tenerse en cuenta que ax al cuadrado es el término cuadrático, mientras que bx es el término lineal y c, el término independiente.
Cuando están presentes todos los términos, se habla de una ecuación cuadrática completa. En cambio, si falta el término lineal o el término independiente, se trata de una ecuación cuadrática incompleta.
 Temas
Temas Resumen
ResumenSobre el concepto
Antes de avanzar con el significado del concepto, se hace necesario descubrir el origen etimológico de las dos palabras que le dan forma:
- Función deriva del latín functio, que es fruto de la suma de dos partes bien diferenciadas: la forma verbal functus, que significa “cumplir”, y el sufijo -tio, que se usa para indicar “acción y efecto”.
- Cuadrática, en tanto, que significa “relativo al cuadrado” y también deriva del latín. Exactamente es el resultado de la combinación de tres componentes léxicos de dicha lengua: la palabra quattuor, que significa “cuatro”; la partícula -atos, que se usa para indicar “que ha recibido la acción”, y el sufijo -tico, cuyo significado es “relativo a”.
En el terreno de las matemáticas se denomina función al vínculo entre dos conjuntos a través del cual a cada elemento del primer conjunto se le asigna un solo elemento del segundo conjunto o ninguno. La idea de cuadrático, por otra parte, también se usa en el ámbito de las matemáticas, aludiendo a aquello relacionado con el cuadrado (el producto de la multiplicación de una cantidad por sí misma).

Una trayectoria balística puede detallarse mediante la función cuadrática.
Características de la función cuadrática
La función cuadrática puede expresarse a través de una ecuación cuya forma estándar es f (x) = ax al cuadrado + bx + c. Suele aparecer en ámbitos como la geometría y la cinemática, entre otros contextos.
La representación gráfica de la función cuadrática, por su parte, se realiza través de una parábola. La orientación de la parábola, el vértice, el eje de simetría, el punto de corte con el eje de las coordenadas y el punto de corte con el eje de las abscisas son características que varían de acuerdo a los valores de la ecuación cuadrática en cuestión.
El vértice es el punto más bajo o más alto de la parábola. En él, se produce una modificación de la dirección. Esto quiere decir que la parábola puede crecer hasta el vértice y luego caer o viceversa. A la línea vertical que atraviesa el vértice y permite segmentar la parábola en mitades iguales se la denomina eje de simetría.
Considerando estas cuestiones, tenemos que señalar que esta parábola puede ser de dos tipos: una parábola convexa o una parábola cóncava. La parábola convexa se identifica porque sus brazos o ramas están orientados hacia abajo, mientras que la parábola cóncava se caracteriza porque esos brazos o ramas se hallan dirigidos hacia arriba. En este sentido, hay que subrayar que la parábola será cóncava cuando a > 0 (positivo). Por el contrario, será convexa cuando a < 0 (negativo). De la misma manera, es interesante saber que las soluciones o raíces de la función cuadrática son fundamentales porque dan a conocer los puntos de intersección de la parábola con respecto al eje de abscisas.
La convexidad y la concavidad en la gráfica de parábola, pues, revelan información importante: cuando la parábola evidencia una apertura hacia arriba, registra un decrecimiento previo al vértice y un crecimiento posterior; en cambio, si la parábola tiene una apertura hacia abajo, su crecimiento es anterior al vértice y su decrecimiento llega tras él.

La función cuadrática se representa gráficamente en el plano cartesiano mediante una parábola.
Los grados
Es importante indicar que la función cuadrática es un polinomio de grado 2. Esto implica que se trata de una función polinómica en la cual el mayor término de grado es siempre de segundo grado.
Hay que recordar que, en un polinomio, su grado equivale al grado más alto de los exponentes de las variables que aparecen en los monomios que lo integran. En la función cuadrática, el polinomio de grado 2 suele aludir a que su grado es exactamente 2, aunque también puede referirse a que el grado máximo es 2.
Ejemplos de función cuadrática
La función cuadrática hace posible el análisis y el modelado de distintos fenómenos que trazan una trayectoria parabólica. Su aplicación se da en ámbitos como la economía, la ingeniería y la física.
Un ejemplo de función cuadrática aparece en la economía cuando se buscan conocer las pérdidas o las ganancias de un comercio. Los cálculos vinculados a la función cuadrática, asimismo, sirven para detallar la trayectoria de un proyectil.
En el terreno de la ingeniería, la función cuadrática contribuye al diseño de puentes, por ejemplo. También sirve para realizar el modelado de los chorros de agua en una fuente, por mencionar otra posibilidad.

