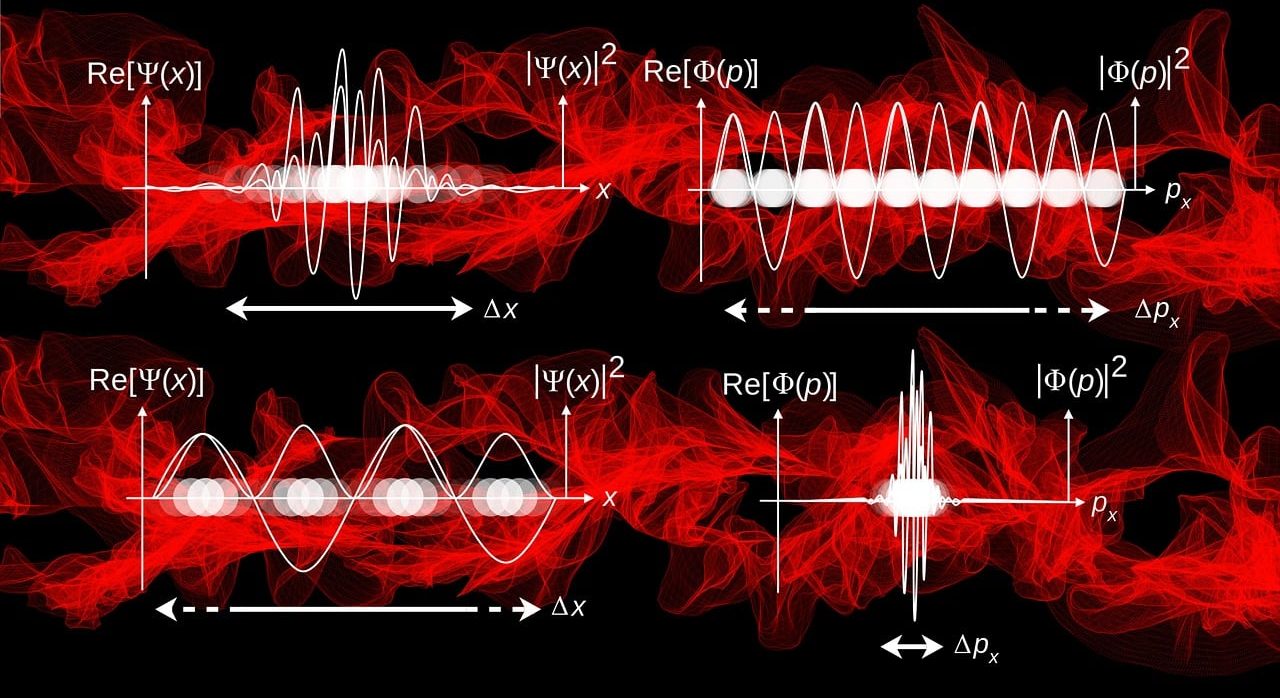
La función de onda, representada a través de la letra griega psi, es una herramienta de carácter matemático capaz de representar el estado de un sistema cuántico.
Función de onda es un recurso que se emplea en el ámbito de la mecánica cuántica con el objetivo de describir el estado físico que presenta un cierto sistema de partículas.
En base a sus particularidades, esta herramienta puede ser concebida como función de cuadrado integrable. Al momento de conseguir una explicación sobre la evolución temporal que posee una función de onda y conocer cómo o cuál es el estado físico de un sistema considerando el intervalo establecido entre un par de medidas resulta útil apelar a la ecuación de Schrödinger.
Teniendo en cuenta el principio de superposición cuántica, pueden ser sumadas y multiplicadas por números de onda diversas funciones de onda y así formar otras constituyendo además un espacio de Hilbert.
 Temas
Temas Resumen
ResumenParticularidades de la función de onda
Existen varias características de la función de onda que permiten reconocer con exactitud sus atributos y sus limitaciones, entre otras cuestiones.
Al examinar su espacio de configuración, por ofrecer precisiones al respecto, se advierte que este recurso que debe responder a un valor único es continuo, finito y unívoco. En el espacio tridimensional, además, sirve para marcar la distribución de probabilidad.
Esta función compleja es útil, según se comprueba en la práctica, para esclarecer cómo es, dentro de un sistema de partículas, el comportamiento de las mismas, así como también es ideal para evidenciar cómo se comportan las partículas en los átomos. Con esta herramienta identificada con una letra griega (psi), incluso, se llega a representar cuán amplia es la probabilidad de hallar, en un momento y en un punto concretos, una determinada partícula.
Cabe resaltar que, en un principio, la noción se gestó desde la perspectiva de la física cuántica más primitiva, época en la cual se consideraba que una partícula podía representarse por medio de una onda física propagada en el espacio. La mirada moderna, en tanto, posiciona a la función de onda como un objeto abstracto apropiado para representar a un elemento vinculado a un espacio de Hilbert que se destaca por una dimensión infinita capaz de agrupar a eventuales estados del sistema.
No se deben perder de vista, por otra parte, las limitaciones que se le atribuyen. Dicen aquellos que se especializan en el tema que ninguna función de onda tiene que poseer un carácter infinito en una región finita y que su pendiente no puede ser indefinida. En x, la pendiente de la función requiere un perfil continuo. También se pretende que sea solución para la ya mencionada ecuación de Schrödiger y ser normalizable (es decir, cuando x está próxima a infinito, la función tiene que acercarse a cero).

Con una función de onda se consigue caracterizar un enlace químico, por ejemplo.
Interpretaciones
La función de onda está sujeta a numerosas interpretaciones. De acuerdo al lineamiento de la mecánica cuántica más ortodoxa, la función de onda debe asociarse a un sistema individual y ser descifrada como estadística. En este contexto, se trata de una ecuación que refiere a cómo se comportan las partículas cuánticas.
Existe, por otra parte, una visión estadística que entiende a la función de onda como un recurso de la mecánica cuántica basado en la probabilidad de hallar una partícula en un espacio puntual. Se dice que es un constructo de índole matemática que no supone la representación de una realidad física y que la función de onda es aplicable a un grupo de partículas o sistemas (es decir, no adaptable de forma individual).
Tampoco hay que dejar de hacer alusión al abordaje positivista; a la interpretación de probabilidad estándar; a la interpretación de Copenhague ni a la teoría de variables ocultas que se vinculan a la función de onda.
Al estudiar las ramificaciones y miradas referidas a la función de onda adquiere relevancia, de igual modo, la interpretación de muchos mundos. En este escenario, la función de onda se extiende en una evolución temporal a lo largo de un proceso, por eso surgen distintas versiones en cuanto a la realidad, donde cada uno de los eventos cuánticos provoca senderos nuevos.

Así como el Big Bang busca explicar cómo surgió el universo, la función de onda constituye un modo de reflejar el estado de un sistema de partículas.
Aplicaciones de la función de onda
La función de onda tiene una gran variedad de aplicaciones. Es una aliada, por ejemplo, de los físicos cuánticos ya que con ella se facilita la comprensión de cómo es el estado físico de un determinado sistema de partículas.
Para tecnologías cuánticas emergentes, tales los casos de la criptografía cuántica y la computación cuántica, también es de suma utilidad. Con ella se revoluciona la manera de procesar información y se torna más sencillo el abordaje de problemas computacionales de marcada complejidad.
Asimismo, es un recurso ventajoso cuando se trata de develar probabilidades y entender su influencia en la dualidad onda-partícula.
En la teletransportación o transporte cuántico, por otra parte, la función de onda es aprovechada para el entrelazamiento de partículas y la transmisión de datos entre ellas.
Al investigar el alcance de la función de onda se comprueba, incluso, su valor dentro de la cosmología cuántica, donde se interpreta como una representación del universo, una herramienta útil para poder analizar qué efecto tiene sobre él la mecánica cuántica.


 Publicado por
Publicado por