El vocablo griego díedros llegó al castellano como diedro, un concepto que se emplea en el ámbito de la geometría. Se denomina ángulo diedro a las porciones espaciales que se encuentran limitadas por un par de semiplanos originados en la misma recta.
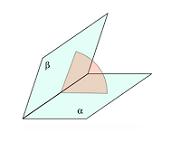
Para representar un ángulo diedro, es necesario recurrir a dos paralelogramos que cuenten con un lado en común. Estas figuras permiten simbolizar los dos semiplanos que, partiendo de una misma arista, dan lugar a esta clase de ángulos.
Recordemos que el paralelogramo se define como un cuadrilátero (un polígono que posee cuatro lados y cuatro vértices) con la característica de que sus dos pares de lados opuestos son iguales y paralelos. Entendemos por lados opuestos, valga la aclaración, a aquellos que no tienen un vértice en común. El aspecto del paralelogramo es muy particular, ya que parece un cuadrado que ha sido deformado; de hecho, los programas de edición gráfica más comunes poseen la opción de alterar de este modo las imágenes para conseguir diferentes efectos.
El otro de los conceptos que aparece relacionado con el de diedro es la arista, el cual también pertenece al ámbito de la geometría. Se trata de un segmento de recta cuyo objetivo es limitar el lado (o la cara) de una figura plana. En la rama de la geometría conocida como geometría del espacio, la cual estudia las figuras con volumen que ocupan lugar, se habla de arista para denominar el segmento en el cual se encuentran dos caras.
A partir de un plano auxiliar que es perpendicular a la recta de origen, se obtiene el ángulo diedro, cuyo valor equivale a la amplitud que alcanza el ángulo menor que producen las semirrectas que pertenecen a los distintos semiplanos.
Puede decirse, en definitiva, que un ángulo diedro es una región espacial formada por dos semiplanos con una recta en común. Las caras del ángulo son dichos semiplanos, mientras que su arista es la mencionada recta común. La medida, por su parte, es la menor de su ángulo rectilíneo.
De acuerdo a sus ángulos, es posible diferenciar entre un diedro cóncavo y un diedro convexo. Los diedros convexos, a su vez, pueden ser obtusos, rectos o agudos. Por otro lado, según las características de sus ángulos rectilíneos, puede hablarse de diedros suplementarios y diedros complementarios.
Dadas las limitaciones de las herramientas disponibles a los alumnos y profesores en las aulas de los colegios y las facultades, la representación de los ángulos diedros en papel y en la pizarra no suele hacerse con la pertinente deformación que causaría en los semiplanos la perspectiva, sino que se dibujan de manera axonométrica.
El sistema para representar figuras gráficamente conocido con el nombre de perspectiva axonométrica consiste en utilizar una proyección cilíndrica o paralela para dibujar volúmenes o elementos geométricos en un plano, de manera tal que sus proporciones (su altura, su longitud y su anchura) se mantengan a lo largo de cada uno de los tres ejes sobre los cuales se proyecta.
En otras palabras, en los libros de geometría y en las fuentes que encontramos en Internet, la representación gráfica del concepto de diedro no posee una perspectiva realista, es decir, la que tendría un objeto en el mundo real. Gracias a este recurso, es posible medir los lados de los semiplanos y la extensión de la arista sin importar la distancia a la que se encuentren del observador, ya que el resultado es siempre el mismo.
La noción de diedro también puede encontrarse en otros terrenos más allá de la geometría. Un centro de escalada de la ciudad chilena de Iquique, una casa de decoración de Madrid (España) y una empresa tecnológica de Zaragoza llevan dicho término en su denominación.
