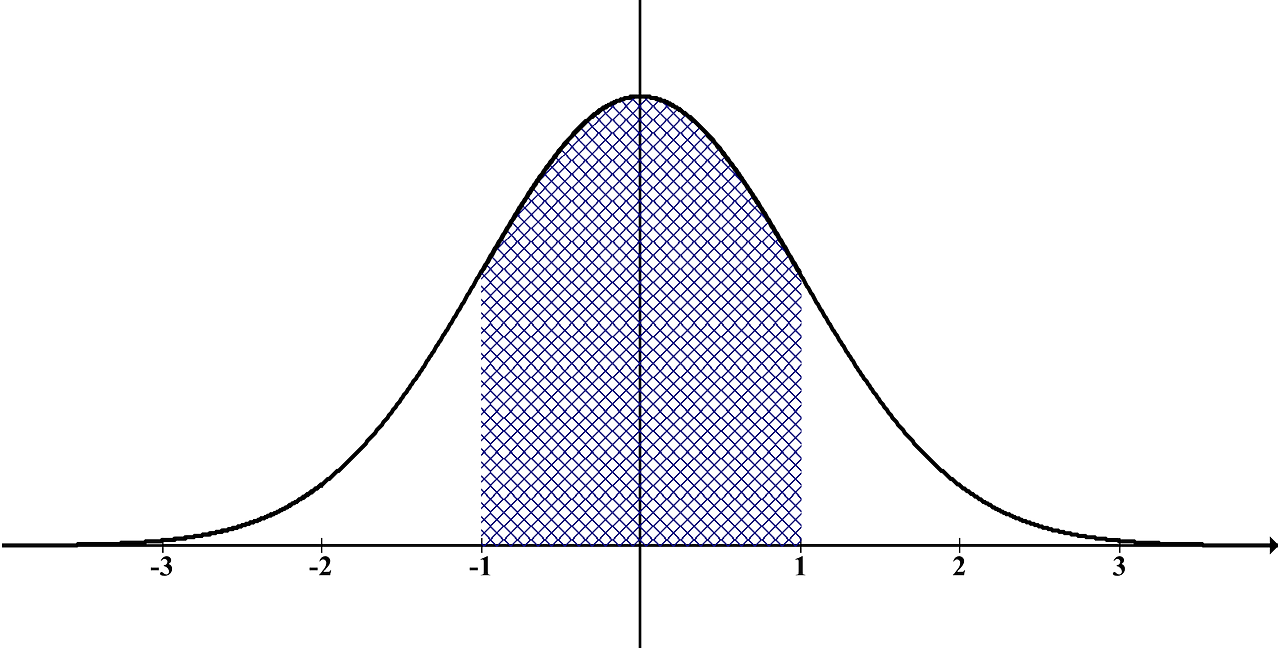
La distribución normal, caracterizada por su forma de campana y su simetría, sirve para analizar datos y como base de pruebas estadísticas.
La distribución normal es un recurso aprovechado en diversas disciplinas como la economía, la medicina, la química y la estadística a fin de modelar fenómenos cuya variabilidad es aleatoria.
Se la señala también como distribución gaussiana o campana de Gauss a raíz de su apariencia, ya que la curva simétrica que caracteriza a esta distribución teórica de probabilidad continua se asemeja a una campana.
Gracias a ella es posible mostrar cómo determinados valores quedan agrupados en torno a un punto céntrico, plasmándose así una distribución de datos que se desarrolla alrededor de la media.
 Temas
Temas Resumen
ResumenCaracterísticas de la distribución normal
La distribución normal, además de exhibir una curva con forma de campana, presenta otras particularidades que vale la pena tener en cuenta.
Uno de sus rasgos distintivos, sin dudas, es su simetría respecto a la media. Al analizarla se observa que, de un lado y del otro del valor central, la forma es idéntica. Esto se debe a que son iguales la media, la mediana y la moda, coincidiendo en el corazón de la distribución.
Con ella, que sirve como base para la estimación, cada prueba de hipótesis o la inferencia estadística, se consigue modelar datos (en especial si se conocen la desviación estándar y la media) y describir fenómenos tanto naturales como sociales.
Es oportuno señalar que, aunque son atípicos, los eventos extremos pueden cuantificarse dado que cada cola de distribución normal decrece o disminuye de manera exponencial.
Importancia y propiedades
La distribución normal es importante tanto en la teoría como en la práctica. En el segmento de estadística resulta esencial, así como también tiene relevancia en muchas especialidades científicas, siendo de gran utilidad al analizar datos biológicos o efectuar un control de calidad, por ejemplo.
En inferencia estadística, la distribución normal es aliado del proceso de modelado de promedios muestrales. De acuerdo al teorema del límite central (TLC), existe una tendencia a la distribución normal en la suma o en el promedio de numerosas variables aleatorias independientes donde se registran varianza y media finitas.

La apariencia de campana propia de la distribución normal sirve para reflejar una distribución simétrica de los datos, que en su mayoría se agrupan en cercanías de la media.
Es interesante poner la lupa, asimismo en la estandarización. En relación a esta cuestión hay que destacar su utilidad al estimar probabilidades empleando una tabla estándar o hacer comparaciones de datos correspondientes a distintas distribuciones normales. Con las transformaciones de puntuaciones a valores Z en el contexto de la distribución normal, una variable aleatoria normal se convierte en una variable normal estándar.
En una distribución normal simétrica, por otra parte, es factible valorar la dispersión de datos apelando a la regla empírica 68-95-99.7. Esta estructura indica, en porcentajes, que alrededor del 68 por ciento de los datos se encuadra dentro de una desviación estándar de la media y cerca del 95 por ciento de los datos está, respecto a la media, dentro de un par de desviaciones estándar, mientras que el 99.7 por ciento de los datos aproximadamente se halla, considerando a la media, dentro de tres desviaciones estándar.
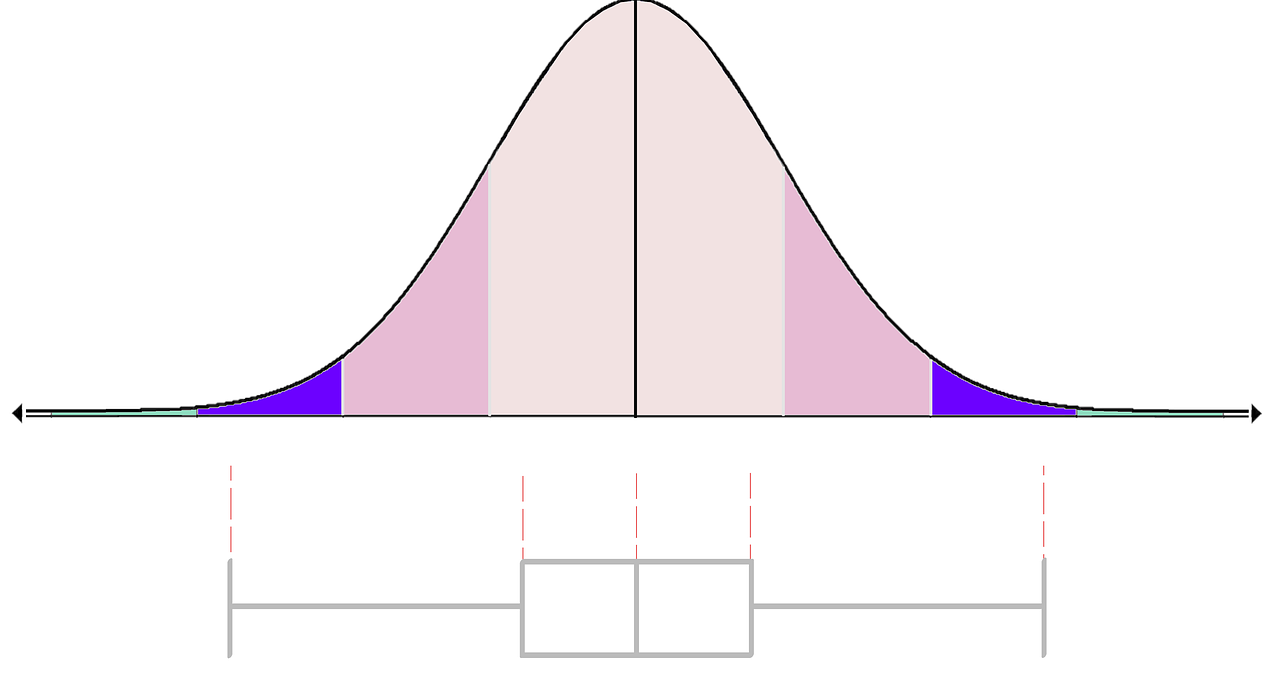
La distribución gaussiana es útil para efectuar análisis de probabilidad o trabajar con regresiones lineales, pruebas de hipótesis e intervalos de confianza.
Ejemplos de distribución normal
La distribución normal se aprovecha en una gran cantidad de rubros, actividades y tareas para el modelado de datos, en especial cuando son simétricos y tienen la tendencia de agruparse en torno a una media.
Por ejemplo: en una empresa dedicada a la fabricación de tornillos se usa como herramienta la regla 68-95-99.7 con el propósito de identificar a las piezas defectuosas que hayan quedado por fuera de los rangos de medición deseados (una desviación estándar calculada en 0.1 centímetros y una longitud media de 6 cm). Así, pues, la distribución normal se aplica al proceso de control de calidad para garantizar el cumplimiento de estándares.
También en establecimientos educativos se determinan criterios para la admisión de alumnos y percentiles en función de puntuaciones específicas en exámenes estandarizados que suelen exhibir una distribución normal.
Otro caso de uso de la distribución normal se da dentro de los mercados y el universo de las finanzas. En pos de hacer una evaluación de riesgos, los inversionistas analizan el retorno promedio (considerando una determinada desviación estándar) de una acción o de otro activo financiero.
Para la realización de estudios médicos por un lado (a fin de evaluar y comparar variables biológicas con el objetivo de plantear rangos normales), así como a la hora de brindar una óptima experiencia de usuario en una página web (diseñando una interfaz digital con un aceptable tiempo de carga) se contempla, igualmente, a la distribución normal.
Es enriquecedor mencionar, incluso, que hay tecnologías emergentes que expanden la aplicación de la distribución normal. Es muy interesante tenerla en cuenta al analizar datos en sensores u otros dispositivos de Internet de las Cosas (IoT) para descubrir anomalías o efectuar un monitoreo preventivo en tiempo real.
Las preferencias de usuarios, en el marco de aplicaciones o programas de inteligencia arficial, están modeladas mediante una distribución normal, que sirve para examinar la variabilidad de predicciones realizadas por un modelo de, por ejemplo, machine learning.


 Publicado por
Publicado por