
La propiedad asociativa aplicada a la teoría de conjuntos permite agrupar subconjuntos en ciertas operaciones sin modificar el resultado final.
Teoría de conjuntos es el nombre de una especialidad fundamental dentro del área de las matemáticas modernas. Esta rama, de gran relevancia para la lógica matemática, se encarga de estudiar las operaciones, relaciones y propiedades entre elementos que integran un conjunto.
Los expertos en informática usan la teoría de conjuntos para estructuras de datos, algoritmos, teoría de la computación y bases de datos, así como en estadística y probabilidad sirve para definir axiomas de probabilidad. En álgebra, teoría de grafos, biología y filosofía también se aprovecha esta herramienta.
Es oportuno señalar que el impulsor principal de la teoría de conjuntos inicial fue el matemático Georg Cantor, quien estuvo inspirado y motivado por ideas y aportes de Bernhard Bolzano y Julius Wilhelm Richard Dedekind. A fin de ganar precisión y minimizar las contradicciones de ese primer sistema, Gottlob Frege buscó fundamentarlo con un postulado propio pero Bertrand Russell terminó hallando en él una contradicción: la llamada paradoja de Russell. Posteriormente, Ernst Zermelo le dio una base sólida a la teoría de conjuntos mediante un modelo axiomático restringido. Ese material fue clave para el surgimiento de la teoría axiomática de conjuntos bautizada como teoría de Zermelo-Fraenkel-Skolem porque en ella intervinieron además Abraham Fraenkel y Thoralf Skolem.
 Temas
Temas Resumen
ResumenImportancia de la teoría de conjuntos
Conocer la teoría de conjuntos y saber aprovecharla es de gran importancia. Esta herramienta permite trabajar en numerosas disciplinas que, para ciertos procesos o cálculos, requieren los fundamentos y el lenguaje de la matemática contemporánea.
Diseñar sistemas, circuitos y algoritmos; organizar y clasificar volúmenes considerables de datos; estudiar paradojas matemáticas y darle una base lógica a funciones y números son algunas de las acciones posibles a partir de ella.
Al aplicarla correctamente se beneficia el aprendizaje ya que favorece la asociación de conceptos y la formación de una red de conocimiento por medio de operaciones lógicas y tareas de inclusión o exclusión según corresponda. Asimismo, la teoría de conjuntos ayuda a resolver problemas en la vida cotidiana, sirve como técnica de estudio y contribuye a la toma de decisiones por estimular el pensamiento lógico y enseñar a trabajar con una agrupación sistemática y estructurada de colecciones de objetos.
En resumen, la teoría de conjuntos es necesaria desde edad temprana porque ofrece recursos para identificar elementos que pertenecen a una misma familia y afrontar desafíos de complejidad variable.

Los números se organizan de acuerdo a jerarquías en la teoría de conjuntos: números naturales y números enteros, y números racionales e irracionales como parte de los números reales, por ejemplo.
Características
La teoría de conjuntos define las nociones de conjunto y elemento. Marca cómo representar las agrupaciones, qué propiedades hay y cuáles son las operaciones posibles.
Se consolida de esta manera la idea de una colección específica de objetos diferentes (elementos) agrupados por tener rasgos o propiedades en común. Los elementos no se repiten ni poseen un orden en particular.
Todos los elementos contemplados en un contexto puntual constituyen el conjunto universal (U), sostiene la teoría de conjuntos. El subconjunto (⊆), en tanto, se forma con parte o la totalidad de los elementos abarcados por el conjunto universal. Puede tratarse de un subconjunto propio (si presenta diferencias respecto al conjunto universal) o de un subconjunto impropio (coincide el subconjunto con el conjunto universal). De no haber elementos, entonces es un conjunto vacío (∅).
Teniendo a la teoría de conjuntos como punto de partida para las clasificaciones es posible diferenciar entre conjunto finito (colección limitada de elementos contables) y conjunto infinito (elementos ilimitados). También se distingue entre conjunto numerable (elementos listados en secuencia) y conjunto no numerable (elementos que resultan incontables, por eso nunca se logra una lista completa).
Es enriquecedor tener presente, por otra parte, que hay propiedades, operaciones y relaciones que rigen la teoría de conjuntos. Se trabaja, de acuerdo a cada caso, con opciones de unión, intersección o pertenencia, así como es factible establecer propiedades conmutativas o asociativas, por indicar algunas alternativas específicas.
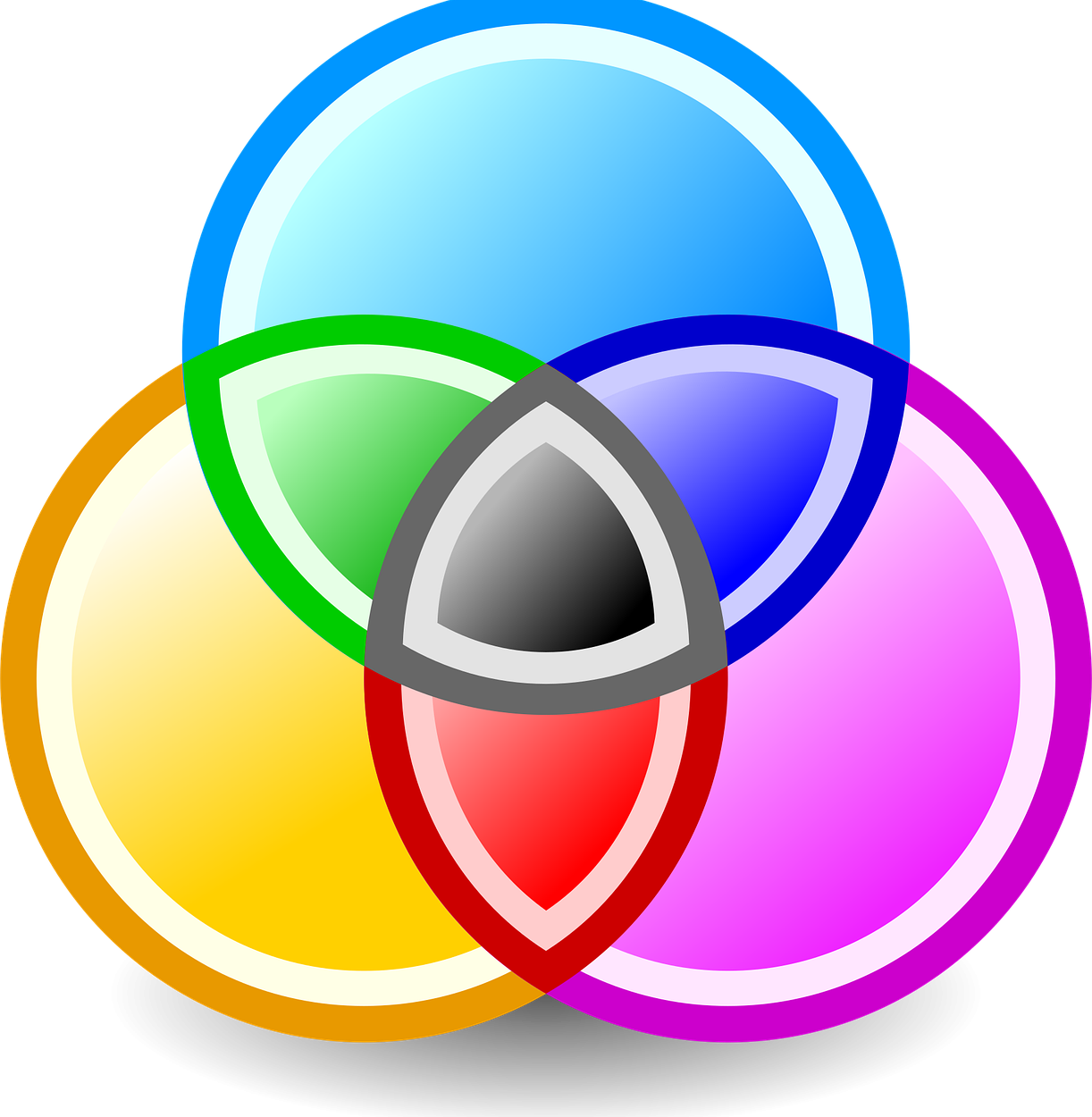
Diagrama de Venn es una herramienta de representación gráfica, generalmente hecha con círculos, para organizar conjuntos y subconjuntos.
Ejemplos de teoría de conjuntos
Con ejemplos de aplicación de la teoría de conjuntos resulta más sencilla comprender la definición teórica de este concepto.
Por señalar un caso fácil de identificar en la vida cotidiana: analicemos el conjunto universal de alimentos. Dentro de él podemos encontrar los subconjuntos de frutas (banana, naranja, manzana), verduras (lechuga, brócoli, espinaca) y legumbres (lentejas, arvejas, garbanzos). Con un diagrama de Venn y llaves se facilita la visualización de cada lista y la relación entre los grupos, que pueden llegar a compartir el tomate (es una fruta que frecuentemente se emplea en ensaladas o acompañamiento como las verduras).
Otra alternativa, teniendo como conjunto universal a los animales. Los subconjuntos pueden ser varios, según el criterio empleado: mamíferos (león, mono, perro…), anfibios (sapo, rana, salamandra…) y reptiles (tortuga, cocodrilo, iguana); animales salvajes (tiburón, jirafa, tigre…) y mascotas (perro, gato, hámster…); animales terrestres, aéreos y acuáticos; vertebrados e invertebrados; omnívoros, carnívoros y herbívoros, etc. Al analizar cada uno de los elementos que pueden incluirse es posible hallar casos de especies que pertenecen simultáneamente a más de un subconjunto (el perro, puntualmente, además de ser un vertebrado terrestre admitido como mascota es un mamífero que puede ser carnívoro u omnívoro, detectándose intersecciones).


 Publicado por
Publicado por