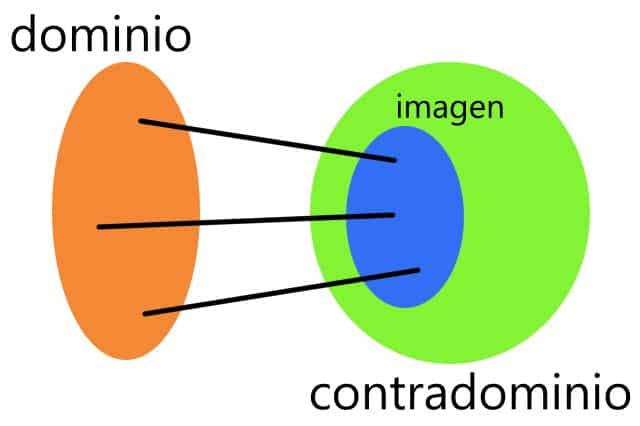
El contradominio es el conjunto de llegada, e incluye la imagen.
La idea de contradominio, también mencionada como conjunto de llegada, conjunto final o codominio, se emplea en el ámbito de las matemáticas. El concepto aparece al aludir a las funciones.
 Temas
TemasFunción matemática
Antes de avanzar, es importante recordar que se denomina función matemática a la relación establecida entre dos conjuntos, mediante la cual a cada elemento que se encuentra en el primer conjunto se le asigna un solo elemento (o ninguno) del segundo conjunto.
Este concepto es de gran importancia en el ámbito de las matemáticas, pero también más allá de sus límites, ya que en nuestro día a día existe un sinfín de relaciones que pueden analizarse como funciones. Seamos o no conscientes de ello, establecemos muchos lazos lógicos entre los elementos que componen nuestra vida, así como aplicamos los fundamentos de la física para movernos y evitar obstáculos al caminar.
Si bien en la etapa estudiantil nos acostumbran a estudiar las funciones como parte de ejercicios pensados previamente por los docentes, de manera que ya existe una solución detectada por ellos, en la práctica se plantean para hallar dicha solución, de manera que conocer sus componentes (dominio, contradominio, imagen, variables, conjuntos de números, etcétera) y aprender a usarlos es fundamental.
Dominio y contradominio
El conjunto de partida es el dominio; el conjunto de llegada, el contradominio. Por lo tanto, si consideramos un conjunto A y un conjunto B, una función es el vínculo que se genera cuando a cada elemento de A (el dominio) le es asignado un único elemento del B (el contradominio).
Tomemos el caso de la función f(x) = 3 . x, con un dominio que, en este caso, es el conjunto {2, 4, 8}. Por lo tanto, el contradominio podría ser el conjunto {6, 12, 24}, ya que la función consiste en multiplicar por tres cada elemento del dominio.
Es importante tener en cuenta que la función es una ley que presenta una correspondencia unívoca. Esto quiere decir que a cada elemento del dominio solamente le puede corresponder un elemento del contradominio.
En el lenguaje coloquial, el dominio es el conjunto que indica aquello que puede entrar en la función, mientras que el contradominio se forma con aquello que es posible que salga. Se llama imagen o rango a lo que efectivamente sale de la función. Cabe resaltar que todas las funciones cuentan con su dominio.
Diferencia con la imagen
Si bien es posible que se confundan los términos imagen y contradominio en algún contexto, su definición técnica los distingue perfectamente: la primera cuenta únicamente con elementos que son valores de salida, mientras que el contradominio puede tener otros, más allá de los que se correspondan con los del dominio.

La imagen raramente coincide con el contradominio.
Veamos un ejemplo para entender mejor esta diferencia: si la función consiste en multiplicar la variable x por 2, entonces podemos afirmar sin temor a equivocarnos que la imagen solamente contiene los números pares; esto se debe a que no existe ningún número impar que sea el producto de una multiplicación por 2 de uno natural (para obtener 3, por ejemplo, debemos multiplicar 1,5 por 2, así como 27 es el resultado de 13,5 por 2, y así sucesivamente). El contradominio, en cambio, es el conjunto de los números naturales, ya que entre ellos encontramos los pares recién mencionados.
Por otra parte, esta diferencia no impide que, en algunos casos, sí exista una total coincidencia entre la imagen y el contradominio. En tal caso, nos encontraríamos ante una función sobreyectiva, suprayectiva, epiyectiva, subjectiva, exhaustiva o suryectiva. En otras palabras, este tipo de función se caracteriza por tener para cada elemento del conjunto de llegada al menos uno de salida. Un ejemplo de los tantos posibles de función sobreyectiva es la siguiente: f(x) = 2 (x + 1).

