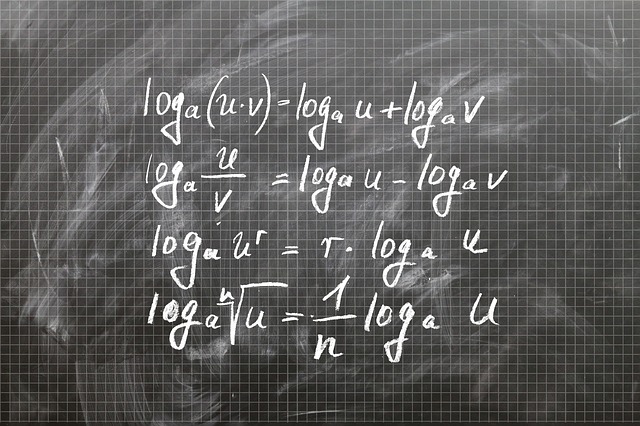
La función logarítmica puede definirse como la función inversa de la exponencial.
El concepto de función tiene múltiples usos. Si nos centramos en las matemáticas, una función es una relación que existe entre dos conjuntos, mediante la cual a cada elemento del conjunto inicial se le asigna un solo elemento del conjunto final (o ninguno). Logarítmico, por su parte, es aquello vinculado a un logaritmo: el exponente al cual se necesita elevar una cierta cantidad para obtener como resultado un número determinado.
A partir de estas ideas, podemos avanzar en la definición de función logarítmica. En estas funciones, a es la base, que tiene que ser positiva y diferente de 1. La forma oficial de leer esta ecuación es la siguiente: «la función de x es igual al logaritmo base a de x». Cabe mencionar que también podría expresarse sin el uso de la expresión f(x), sino con una variable tal como y, ya que de este modo podríamos reflejar con mayor claridad que el resultado es un elemento diferente, de otro conjunto.
Es importante señalar que la función logarítmica es la función inversa de la función exponencial: aquella que se representa con la ecuación f(x) = aˣ
 Temas
TemasCaracterísticas de una función logarítmica
Entre las principales características de una función logarítmica, podemos mencionar que su dominio (su conjunto de partida o inicial) son los números reales positivos. Se trata de una función continua, cuyo recorrido es R (las imágenes que se obtienen de aplicar la función corresponden a cualquiera de los elementos del conjunto formado por los números reales).
Otra propiedad es que la función logarítmica de la base resulta igual a 1 en todos los casos. Las funciones logarítmicas, por otra parte, pueden ser crecientes o decrecientes, así como convexas o cóncavas, según el valor de la base. Para saber si son crecientes, basta con observar si a es mayor a 1; por otro lado, si es mayor a 0 y menor a 1, entonces es decreciente.
Continuando con las propiedades de la función logarítmica, podemos decir que en la gráfica siempre encontramos los siguientes dos puntos: (1, 0) y (a, 1), entendiendo estas duplas como valores en los ejes X e Y, o sea el horizontal y el vertical, respectivamente. La función logarítmica también se considera inyectiva.

La función logarítmica de la base siempre resulta igual a 1.
Las funciones inyectivas
En el ámbito de las matemáticas, se conoce con el nombre de función inyectiva a aquélla en la cual a cada elemento del codominio le corresponde solamente uno del dominio. Dicho en otras palabras, en una función de este tipo, al que también pertenece la logarítmica, no se puede dar el caso de que más de un elemento del primer conjunto tenga la misma imagen.
Al graficar una función logarítmica obtenemos un resultado simétrico al de la función exponencial si tomamos en cuenta la bisectriz de los cuadrantes primero y tercero. Se entiende por bisectriz la semirrecta que nace en el vértice de un ángulo y lo corta en dos partes idénticas. La razón de este fenómeno es que ambas son inversas o recíprocas entre sí.
La función logarítmica y la base o argumento
Las funciones logarítmicas, en definitiva, son aquellas en cuya ecuación la variable es la base o argumento de un logaritmo. Para resolver estas ecuaciones, por lo general se trata de lograr la conversión de la ecuación logarítmica en otra que resulte equivalente pero que carezca de logaritmo.
En algunos casos, la conversión pone la base del logaritmo como la de una potencia elevada a la x e iguala este término a y. Por ejemplo, si tenemos una función de x en la cual la base es 2, para cada elemento del codominio deberemos buscar qué número es igual a él si lo elevamos al cuadrado.

