El término obtuso proviene del latín obtūsus, a su vez derivado del verbo obtundĕre (que puede traducirse como “embotar” o “despuntar”). La noción se emplea de distintas maneras de acuerdo al contexto.
La primera acepción de obtuso mencionada por la Real Academia Española (RAE) en su diccionario alude a aquello que es romo; es decir, que no tiene punta. Un objeto obtuso, en este marco, carece una terminación puntiaguda. Por ejemplo: “La pericia determinó que la víctima fue golpeada con un elemento obtuso”.
Es más habitual la utilización de obtuso para hacer referencia al individuo lerdo o bruto. El sujeto obtuso, por lo tanto, tiene dificultades para comprender o razonar cuestiones que resultan sencillas para la mayoría. El concepto además califica a aquél que es torpe, limitado o tonto: “El dueño de la empresa es un hombre obtuso que heredó la fortuna de sus padres”, “No seas obtuso y escucha a tu entrenador, que sabe de lo que te está hablando”, “Estamos a merced de un gobierno obtuso que no logra resolver los problemas económicos más urgentes”.
En el terreno de la geometría, aparece la idea de ángulo obtuso. Así se denomina al ángulo que mide más de 90° pero menos de 180°. El ángulo obtuso, de este modo, es mayor que el ángulo recto y menor que el ángulo llano.
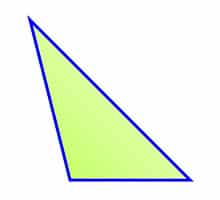
Al triángulo que cuenta con un ángulo obtuso y dos ángulos agudos se lo llama triángulo obtuso o triángulo obtusángulo. Dado que los ángulos interiores de un triángulo siempre tienen que sumar 180°, no es posible que un triángulo presente más de un ángulo obtuso.
El triángulo obtuso pertenece al grupo de los llamados triángulos oblicuángulos u oblicuos, los cuales se caracterizan por no contar con ningún ángulo recto (de 90°). Esto acarrea que no pueda resolverse haciendo uso del teorema de Pitágoras tal y como podemos hacer con los triángulos rectángulos; por el contrario, su resolución exige la aplicación de leyes de senos o de cosenos, según el tipo de triángulo.
Otro de los triángulos que se encuentran en este grupo es el agudo, el cual se compone de tres ángulos menores a 90°, es decir, agudos, y esto le da el nombre. En cualquier triángulo existe el concepto de centroide (o baricentro), que se define como la intersección de todos los hiperplanos que cortan el objeto (en este caso, el triángulo) en dos partes de volumen igual.
Al hablar del centroide de los triángulos, debemos mencionar las medianas (también conocidas como transversales de gravedad), los tres segmentos que van desde cada uno de los vértices hasta el punto medio de su lado opuesto. En otras palabras, si cortamos cada lado a la mitad, la mediana se traza desde allí hacia el vértice opuesto, es decir, el único que no toca ese lado.
También está el incentro, que se consigue dibujando un círculo que toque los tres lados del triángulo sin salirse del mismo, y luego identificando su punto central. El ortocentro, en cambio, es el punto en el cual se cruzan las rectas que contienen las alturas del triángulo. El circuncentro, por último, también se denomina circunferencia circunscrita y se obtiene trazando un círculo que pase por todos los vértices de una figura y la contenga en su interior.
Cabe mencionar que estos últimos dos conceptos distinguen el triángulo obtuso del agudo, ya que en este último se observa en su interior, mientras que en el primero, en su exterior. Para calcular las alturas antes mencionadas, debemos dibujar un segmento perpendicular desde cada lado hacia el vértice opuesto; mientras que en un triángulo agudo la intersección se da en el interior, en uno obtuso tiene lugar fuera del mismo, y esto explica la diferencia anterior.
