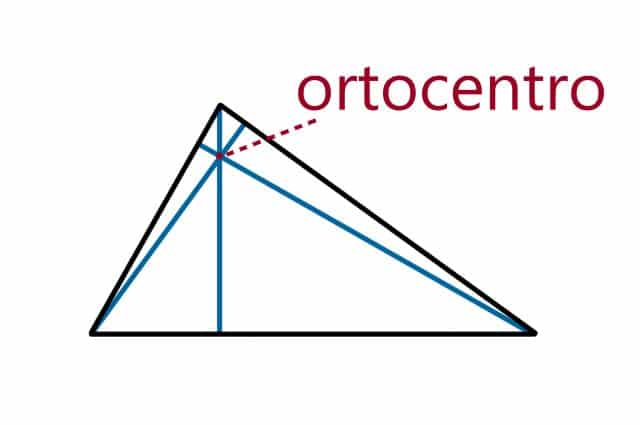
Las alturas del triángulo convergen en el ortocentro.
La noción de ortocentro se emplea en el ámbito de la geometría. Así se denomina al punto donde las alturas de un triángulo se cruzan.
 Temas
TemasUbicación del ortocentro
El punto en el cual las tres alturas se cortan es el ortocentro. Dado que no se trata de un punto arbitrario dentro de la figura, sino de uno que puede hallarse mediante cálculos exactos, se puede usar de referencia tanto como los vértices para ubicar el triángulo en el espacio, por ejemplo. La ubicación del ortocentro depende de las características del triángulo.
En un triángulo obtusángulo (que dispone de un ángulo obtuso y dos agudos), el ortocentro se encuentra fuera de la figura. Si el triángulo es rectángulo (tiene un ángulo recto), el ortocentro resulta coincidente con el vértice del ángulo de 90°. En el caso de los triángulos acutángulos (todos sus ángulos son agudos), el ortocentro se sitúa dentro de la figura.
Resumiendo, puede decirse que, en los triángulos, la altura es una recta que atraviesa un vértice y es perpendicular al lado opuesto. Cada uno de los triángulos cuenta con tres alturas: el punto donde se encuentran las alturas recibe la denominación de ortocentro, que puede localizarse dentro o fuera del propio triángulo.
En los triángulos equiláteros (cuyos lados miden lo mismo), el ortocentro, el circuncentro, el baricentro y el incentro coinciden en un punto interior que se halla a idéntica distancia de los tres vértices. En los triángulos no equiláteros, en cambio, el ortocentro, el circuncentro y el baricentro se posicionan alineados y comprendidos en la llamada recta de Euler. Una propiedad indica que la distancia del ortocentro al baricentro duplica la distancia que existe entre el baricentro y el circuncentro.
Alturas del triángulo
Es importante señalar que cada triángulo tiene tres alturas. Estas alturas son las rectas que permiten unir un vértice con su lado opuesto, siendo perpendiculares a dichos lados.
El triángulo es una figura tan usada como particular, ya que a primera vista podemos consierarla «simple», por ser fácil de dibujar. Sin embargo, cuando la analizamos desde un punto de vista matemático, el nivel de complejidad aumenta considerablemente. Por ejemplo, mientras que para calcular la superficie de un rectángulo basta con multiplicar dos de sus lados (que sean adyacentes), en el caso del triángulo debemos multiplicar su base por su altura y luego dividir el resultado por 2.
Ahora bien: recién mencionamos el término «altura», como una propiedad singular del triángulo, a pesar de que más arriba hablamos de las tres que posee esta figura geométrica. La solución a esta confusión es muy sencilla: debemos escoger de forma arbitraria una de las tres para asignarle su valor a la variable altura de la ecuación, y el lado perpendicular de la misma se convierte en la base.
Nótese que esta altura debe convertir el triángulo en dos triángulos rectángulos, de manera que solamente es posible hallarla en los otros tipos: para los triángulos rectángulos su base y su altura coinciden con sus catetos menor y mayor, respectivamente.
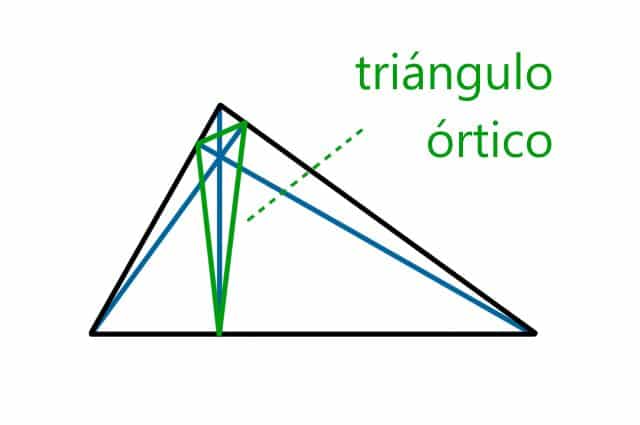
Triángulo «órtico» o «pedal» del expuesto más arriba
Triángulo órtico
Una de las peculiaridades del ortocentro es que nos permite determinar un nuevo triángulo dentro del principal. Se trata del triángulo órtico, el cual se forma uniendo los tres puntos desde los cuales parten las alturas antes definidas. Otro nombre que recibe esta figura es triángulo pedal, y no puede generarse en un triángulo rectángulo.
Estos puntos también reciben el nombre de pies, y son las proyecciones de cada uno de los tres vértices sobre su lado opuesto. Más arriba hablamos de incentro (el punto en el que se cruzan las bisectrices de los ángulos internos); pues el incentro de un triángulo órtico coincide con el ortocentro del que lo contiene.

