El término que ahora vamos a analizar es interesante recalcar que está formado por la unión de dos vocablos que tienen su origen etimológico en lenguas antiguas. Así, límites procede de la palabra latina limes, que es el genitivo de limitis que puede traducirse como borde o frontera de algo.
Por su parte, matemáticos es una palabra que tiene su citado origen en el griego y concretamente en el término mathema. Este puede definirse como el estudio de un tema o asunto determinado.
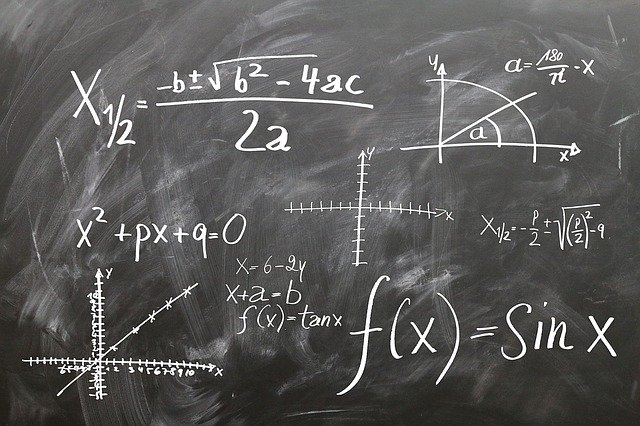
La idea de límite matemático tiene diferentes usos.
 Temas
TemasQué es un límite
La división que marca una separación entre dos regiones se conoce como límite. Este término también se utiliza para nombrar a una restricción o limitación, al extremo que se puede alcanzar desde el aspecto físico y al extremo a que llega un periodo temporal.
Para la matemática, un límite es una magnitud a la que se acercan progresivamente los términos de una secuencia infinita de magnitudes. Un límite matemático, por lo tanto, expresa la tendencia de una función o de una sucesión mientras sus parámetros se aproximan a un cierto valor.
La noción de límite matemático
Una definición informal del límite matemático indica que el límite de una función f(x) es T cuando x tiende a s, siempre que se puede hallar para cada ocasión un x cerca de s de manera tal que el valor de f(x) sea tan cercano a T como se pretenda.
No obstante, además del límite citado, no podemos obviar que existen otros muy importantes en el ámbito de las Matemáticas. Así, también se puede hablar del límite de una sucesión que puede ser existente o único y divergente, en el caso de que los términos de aquella no converjan en ningún punto.
Los límites matemáticos se asocian a las funciones.
De la misma manera, también hay que hablar de otra serie de límites matemáticos tales como el límite de una sucesión de conjuntos o el de espacios topológicos. Entre estos últimos están los que hacen referencia a los filtros o a las redes.
Finalmente tampoco podemos pasar por alto la existencia de lo que se conoce como Límite de Banach. Este último, que recibe el nombre del matemático polaco Stefan Banach, es aquel que gira entorno a lo que se conoce como espacio de Banach. Este es una pieza fundamental dentro de lo que es el análisis funcional y puede definirse como el espacio donde están funciones que cuentan con una dimensión infinita.
Utilidad del concepto
Al igual que otros conceptos matemáticos, los límites cumplen con diversas propiedades generales que ayudan a simplificar los cálculos. Sin embargo, puede resultar muy difícil comprender esta idea ya que se trata de un concepto abstracto.
En matemática, como ya vimos, la noción está vinculada con la variación de los valores que toman las funciones o sucesiones y con la idea de aproximación entre números. Esta herramienta ayuda a estudiar el comportamiento de la función o de la sucesión cuando se acercan a un punto dado.
La definición formal del límite matemático fue desarrollada por diversos teóricos de todo el mundo a lo largo de los años, con trabajos que constituyeron la base del cálculo infinitesimal.


 Publicado por
Publicado por