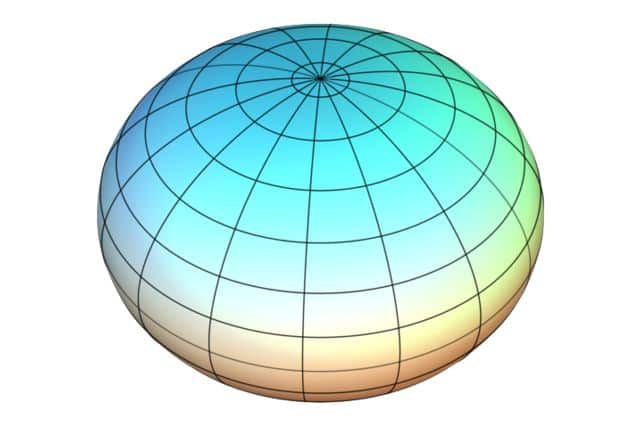
El esferoide es una superficie similar a la esfera, pero no todos sus puntos son equidistantes del centro.
El vocablo griego sphairoeidḗs llegó al latín como sphaeroīdes. Ese es el antecedente etimológico más cercano de esferoide, un término de nuestra lengua que alude a un cuerpo cuya forma es similar a la de una esfera.
 Temas
TemasParecido a una esfera
Se llama esfera, por su parte, al sólido que se encuentra definido por una superficie de tipo curvo, cuyos puntos son equidistantes del centro. Los esferoides, en definitiva, son parecidos a las esferas.
Un esferoide es un elipsoide de revolución: se genera con la rotación de una elipse en torno a un diámetro principal.
Otros cuerpos celestes y objetos astronómicos también forman parte del grupo de los esferoides. Entre ellos podemos nombrar a Haumea (un planeta enano) y a Tetis (una luna de Saturno).
La ecuación cartesiana de esta superficie tan particular es la siguiente: (x2 + y2) / a2 + z2 / c2 = 1. Para que ésta tenga validez, el centro del esferoide debe ubicase en el origen mismo de las coordenadas cartesianas. Las variables a y c representan sus semiejes, y el segmento c se encuentra en el eje Z (el cual suele asociarse con la profundidad de las figuras tridimensionales).
Clasificación
Existen distintas clases de esferoides según sus características y propiedades. Al eje de simetría, que se ubica en el eje Z de las coordenadas cartesianas, se lo nombra con la letra C, mientras que al eje que es perpendicular al eje de simetría se lo llama A.
Cuando C es menor que A, se trata de un esferoide oblato. En cambio, si C es mayor que A, el esferoide es definido como oblongo. Es importante aclarar que si C y A son iguales, la superficie en cuestión es una esfera.
El esferoide oblato presenta sus planos achatados. Diversos planetas exhiben forma de un esferoide oblato, incluso la Tierra. El esferoide oblongo, por otro lado, tiene un diámetro ecuatorial menor que el eje polar, como en el caso de la pelota que se emplea en el fútbol americano.
Haumea
Este planeta enano se halla más lejos de la órbita de Neptuno, en el denominado cinturón de Kuiper. Si bien para el año 2003 ya se conocía, recién en 2008 fue clasificado adecuadamente y bautizado por la Unión Astronómica Internacional (UAI). Su nombre es el mismo de la diosa de la natalidad perteneciente a la mitología de Hawái.
Con respecto a su descubrimiento, lo llevó a cabo en 2003 un grupo de investigadores a cargo del astrónomo español José Luis Ortiz Moreno, en el Observatorio de Sierra Nevada, ubicado en la provincia de Granada. Dado que al año siguiente otro equipo aseguró haberla descubierto primero, en este caso uno estadounidense bajo la dirección de Mike Brown, la UAI no reconoció oficialmente a ninguno de los dos. Sin embargo, en su propia base de datos y en otras fuentes fiables figura el primero.

Tetis, una luna de Saturno, es un esferoide.
Tetis
Como se menciona más arriba, Tetis es una de las lunas de Saturno. Más específicamente, se trata de la quinta de mayor tamaño: su diámetro aproximado es de 1060 kilómetros. Se encuentra a 294 619 kilómetros de distancia de Saturno. Lo descubrió el astrónomo francés Giovanni Domenico Cassini en el año 1684. De los satélites más grandes del sistema solar, es el de menor densidad, porque su composición es mayoritariamente de hielo de agua.
Una de las características de este satélite esferoide es que presenta muchos cráter y diversas fallas extensas. El cráter más grande se conoce como Odysseus, y su diámetro aproximado es de 400 kilómetros; su falla más extensa, por otra parte, es Ithaca Chasma, con una longitud que supera los 2000 kilómetros. Si bien no ha sido probado, se cree que existe una conexión entre estas dos inmensas estructuras.

