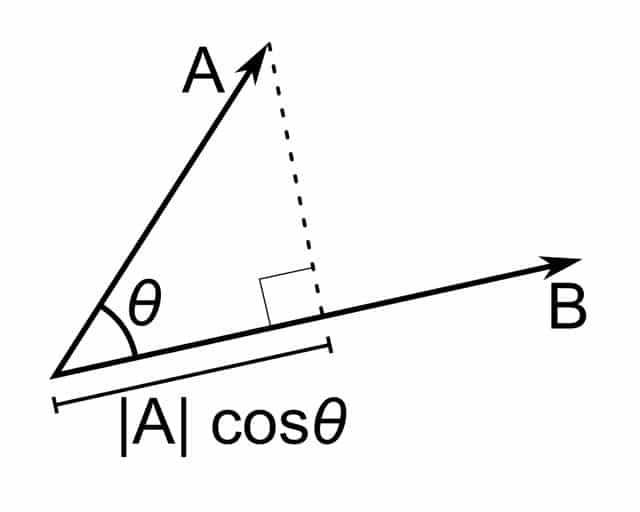
El producto escalar en un espacio euclídeo equivale al de sus módulos por el coseno del ángulo
En el terreno de las matemáticas, se denomina producto al resultado de una multiplicación. La idea de escalar, en tanto, puede emplearse para nombrar al número que posibilita la descripción de un fenómeno con magnitud, aunque dejando de lado la dirección del vector.
Es importante considerar antes de avanzar que un vector es una magnitud que exige la consideración, además de su cuantía, de su sentido, dirección y punto de aplicación.
 Temas
TemasDe vectores a un número
Se conoce como producto escalar, en este marco, a la operación del álgebra que parte de dos secuencias numéricas con la misma longitud (que suelen tener la forma de vectores) y arriba a un único número.
También llamado producto punto, producto interior o producto interno, el producto escalar se obtiene al sumar los productos de las entradas de un par de secuencias numéricas. El resultado no es un vector, sino un escalar.
Puede afirmarse que el producto escalar de un vector a→ y un vector b→ (a→ ⋅ b→) arroja como resultado un número (el escalar) tal que a→ ⋅ b→ = (a→) ⋅ (b→) ⋅ cos(α), siendo α el ángulo que componen los dos vectores (a→ y b→).
Esto nos permite sostener que, para la geometría, el producto escalar es la multiplicación de las magnitudes euclidianas de dos vectores y el coseno del ángulo que forman ambos.
Condiciones y casos especiales
Si los vectores son paralelos y comparten la misma dirección, el producto escalar equivale a la multiplicación de los módulos. En cambio, si el sentido es diferente, se obtiene multiplicando sus módulos pero agregando el signo negativo. Para que sean paralelos, el ángulo que se forma entre ambos debe ser de 0 (ya sea grados sexagesimales o radianes) o bien de pi radianes (o 180 grados sexagesimales). Esta equivalencia se explica porque el coseno de dos vectores paralelos vale 1, de manera que al multiplicarlo por los módulos no afecta su producto escalar.
En el caso de los vectores perpendiculares, el ángulo formado es de 90º y el producto escalar resulta igual a 0. Esto se relaciona con el hecho de que el producto escalar también se puede igualar a la multiplicación del módulo de uno de los dos por la proyección del otro sobre éste; en el caso de dos vectores perpendiculares, la proyección de uno sobre el otro siempre será 0, de manera que no importa cuál sea el otro valor, el producto también será 0.
Para entender un poco mejor este caso especial, pensemos que la proyección es similar a «la sombra» de un vector sobre otro si la fuente de luz es perfectamente perpendicular al segundo; pues esta sombra sería imperceptible (de extensión nula) si el primero fuera paralelo al haz de luz. En términos más técnicos, los vectores perpendiculares entre sí también se conocen por el nombre de ortogonales. Yendo en sentido contrario, si sabemos que el producto escalar de dos vectores es cero, podemos asumir que se trata de de vectores ortogonales.
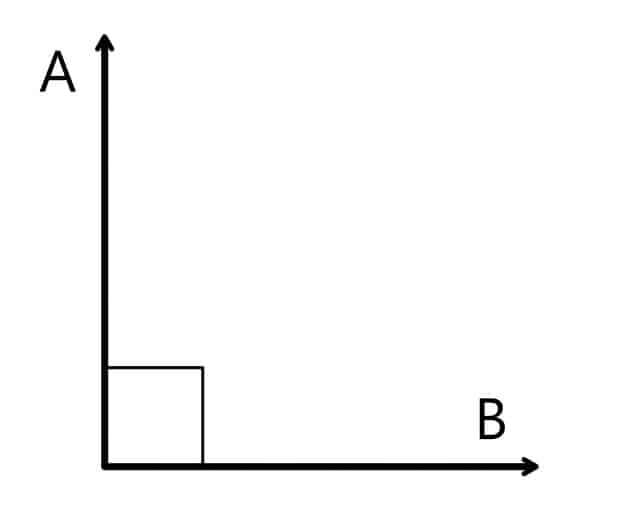
Si los vectores son perpendiculares, el producto escalar vale 0
Propiedades
El producto escalar no deja de ser el resultado de una multiplicación, por más que sea más compleja que la de dos o más números naturales, por ejemplo. Por ello, ambas operaciones comparten las siguientes propiedades: conmutativa, distributiva y asociativa. La primera de las tres es la más conocida y fácil de entender: afirma que el orden de los factores no altera el producto. Dicho de otra manera, obtendremos el mismo resultado siempre que multipliquemos los mismos vectores, sin importar su orden.
La segunda requiere la multiplicación de un vector por la suma de dos o más. En este caso, es posible extraer los sumandos uno a uno, multiplicándolos por el primer vector y creando una suma de estos productos que será equivalente a la primera ecuación: A . (B + C) = A . B + A . C Por último, la propiedad asociativa nos dice que si tenemos la multiplicación de un escalar por un producto de dos vectores es posible convertir la ecuación en el producto de dicho escalar por cualquiera de los vectores y luego multiplicarlo por el restante: e(B . C) = eB . C = B . eC

