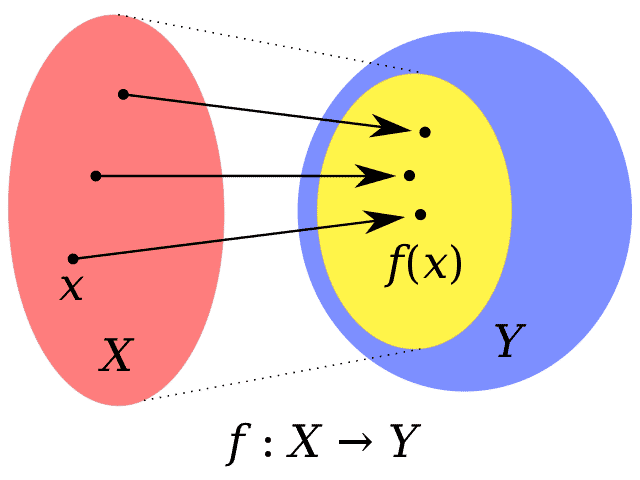
El conjunto imagen (amarillo) es un subconjunto del codominio (violeta).
La idea de rango de una función se utiliza en el ámbito de las matemáticas. La expresión suele referirse a la imagen de la función, aunque también puede aludir al codominio.
 Temas
TemasLos valores de la variable
Por lo general, los documentos y los libros académicos de mayor antigüedad apelan al término rango para centrarse en el codominio de la función. En cambio, las publicaciones más recientes recurren al rango de una función con la intención de hacer mención a la imagen. Por eso es imprescindible prestar atención al contexto para no incurrir en un error a partir de un malentendido.
Actualmente, en definitiva, el rango de una función se relaciona al conjunto de los valores reales que adquiere la variable f(x). El cálculo del rango de una función requiere determinar cuál es el dominio de su función inversa.
Mientras que el dominio de la función f(x) equivale al conjunto de los valores para los cuales dicha función se encuentra definida, el rango de la función f(x) es el conjunto de los valores que f toma.
La imagen
De este modo, cuando el rango de una función se vincula a la imagen, se trata del conjunto que incluye la totalidad de los resultados de dicha función. En este sentido, es importante tener en cuenta que la imagen constituye un subconjunto del codominio.
Es importante señalar que el conjunto al que nos referimos de esta manera no siempre tiene la misma cantidad de elementos que el dominio, ya que en algunos casos más de un elemento del primero tiene como imagen el mismo. Supongamos que tenemos un conjunto con los números del 1 al 10 y deseamos pasarlos por una función que nos devuelva si son pares o impares; el conjunto imagen será en este caso muy pequeño, ya que simplemente tendrá estos dos valores, para cada uno de los cuales habrá varias relaciones con los del dominio.
También puede darse el caso en el cual el segundo conjunto no sea directamente la imagen del primero, sino que ésta la encontremos como un subconjunto de éste. Esto se da si uno o más de sus elementos no son imagen de ninguno de los valores del primero. Tal sería el caso de un conjunto con los nombres de ciertas personas y otro con una serie de nacionalidades, si este último tuviera algunas que no pertenecieran a ninguna de las personas.
Y este ejemplo nos sirve para establecer una diferencia principal entre imagen y codominio, más allá de que ambos se relacionen con el concepto de rango de una función: la primera siempre es un subconjunto del segundo, aunque sea uno que incluya todos sus elementos. Hablando en términos meramente matemáticos, si una función dada tiene como codominio los números reales pero su ecuación consiste simplemente en elevar una variable al cuadrado, la imagen no incluirá los números negativos, de manera que será tan sólo una parte del codominio.
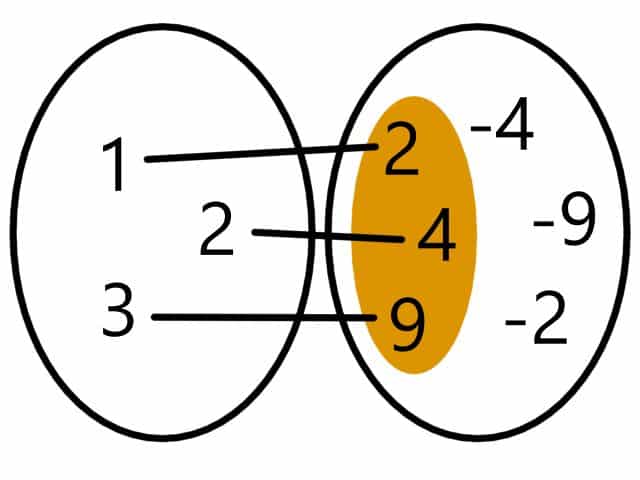
En este ejemplo, los números negativos del codominio no forman parte de la imagen
El codominio
El rango de una función aplicado al codominio, en tanto, está asociado al conjunto de los números complejos (en el caso de la rama conocida como análisis complejo) o al de los números reales (en el análisis real).
Otros nombres por los que se conoce el codominio son recorrido, conjunto de llegada y contradominio. Como mencionamos más arriba, se trata del conjunto en el que podremos encontrar los valores de salida de la función. Es como si la propia definición de la función nos indicara la zona en la que podremos hallar los resultados para evitar que perdamos el tiempo mirando en otras, pero no nos indicara exactamente cuáles de ellos nos servirán. La imagen representan el final de esta búsqueda.

