
La secante es recíproca del coseno.
Secante es una palabra clave en trigonometría pero el concepto no se limita al ámbito matemático. Abreviada como (sec) y resumida por la fórmula sec θ = 1 / cos θ, la secante es la función periódica recíproca del coseno. Por otra parte, tal como se advierte al consultar el diccionario de la Real Academia Española (RAE), funciona a nivel general como un adjetivo con distintas acepciones (existe el papel secante y una técnica de vóley bautizada como secante o sprawl, por citar dos referencias). El vocablo se emplea usualmente para identificar a la superficie o línea que corta a otra. En trigonometría, secante es la razón inversa de la función coseno de un arco o ángulo.
Se trata de una de las funciones trigonométricas fundamentales. Esta función trigonométrica surge en un triángulo rectángulo como el cociente resultante de la longitud de la hipotenusa y la de la base del citado triángulo.
Conocer qué es la secante, sus características, la gráfica de la función secante y su importancia permite saber para qué sirve la secante y cómo se la aplica en ingeniería eléctrica, física y cálculo integral, por ejemplo. Es imprescindible, incluso, para resolver integrales y comprender identidades trigonométricas relevantes. Por eso a lo largo de este artículo indicaremos cuándo conviene usar secante, detallaremos la definición geométrica de la secante y aludiremos a ella como razón trigonométrica.
 Temas
Temas Resumen
ResumenCaracterísticas de la secante
Las características de la secante deben conocerse porque ayudan a entender la gráfica, el comportamiento y la utilidad práctica de dicha función. Es una herramienta clave en ingeniería, matemáticas, arquitectura y física.
La función trigonométrica secante resulta esencial para, por medio de la sustitución trigonométrica, simplificar integrales complejas. También permite hacer cálculos de longitudes inclinadas y modelar fenómenos periódicos que presentan un comportamiento recíproco en relación al coseno.
Al analizar las propiedades de la función secante o sus cualidades principales, además de su definición como sec x = 1 / cos x adquieren notoriedad su dominio (abarcando los números reales con excepción de aquellos para los cuales cos x = 0) y su rango. Su periodicidad (con 2π como período fundamental) y su simetría sec(-x) = sec x en función par también constituyen informaciones enriquecedoras.
Observando la gráfica correspondiente a sec x se advierten curvas de estilo infinito con apariencia de U que se separan entre sí a través de asíntotas verticales. La gráfica resulta simétrica en relación al eje vertical.
La secante es una de las funciones trigonométricas básicas.
Definición y uso en el triángulo rectángulo
La secante (sec), que se define como sec θ = 1 / cos θ o sec θ = hipotenusa / cateto adyacente, en un triángulo rectángulo se obtiene a partir de la hipotenusa (así se identifica al lado que se opone al ángulo recto y que puede determinarse si se conocen el ángulo y el cateto adyacente) y del cateto adyacente (aquel que conforma el ángulo agudo y que se puede averiguar conociendo la hipotenusa). En triángulos rectángulos, la secante también facilita el proceso de encontrar ángulos o lados desconocidos.
Cabe destacar que las razones trigonométricas son seis: seno, coseno, cosecante, secante, tangente y cotangente. Sirven para relacionar cada uno de los lados del triángulo con ángulos específicos, trabajar con proyecciones horizontales y determinar distancias verticales, calcular ángulos de elevación, depresión o inclinación y hallar soluciones a dificultades o problemas profesionales o domésticos que se presentan en la vida cotidiana (como el desafío de medir grandes alturas y distancias de navegación).
Identidades trigonométricas con secante
Las identidades trigonométricas con secante son imprescindibles en ecuaciones trigonométricas, cálculos integrales, demostraciones y trigonometría.
Antes de detallarlas es enriquecedor tener presente que una identidad trigonométrica es una relación de igualdad que se establece entre funciones trigonométricas. Esta ecuación basada en razones trigonométricas se cumple en cada uno de los valores de la variable.
Las más básicas son las identidades recíprocas: sec θ = 1 / cos θ. Las más utilizadas, en tanto, son las identidades pitagóricas (1 + tan² θ = sec² θ y sec² θ − tan² θ = 1). También se aprovechan las identidades de producto recíproco (o de productos que dan 1 como el caso de sec θ · cos θ = 1, ideal para simplificaciones), las identidades de paridad (ángulos negativos, siendo la secante una función par) y las identidades de cofunción sec(π/2 − θ) = csc θ y sec(π/2 + θ) = −csc θ.
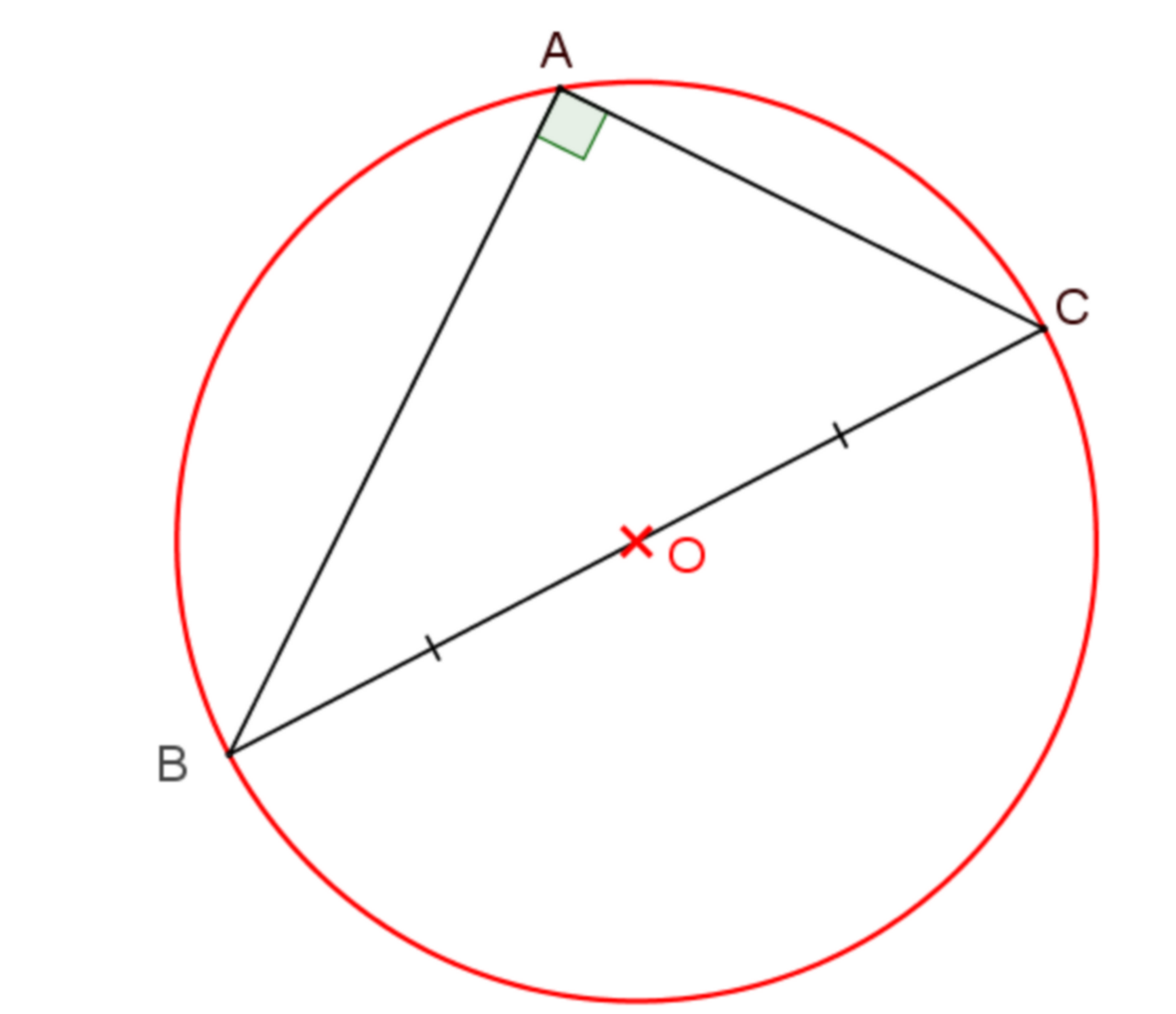
En un triángulo rectángulo, la secante sirve para calcular un lado desconocido y es clave para, combinada con las demás razones trigonométricas, resolver triángulos de manera completa.
Aplicaciones básicas
Además de aprender qué significa secante en la teoría es conveniente saber cuáles son las aplicaciones básicas de la secante en diferentes ámbitos.
En geometría básica se utiliza la secante en triángulos rectángulos para establecer la longitud de la hipotenusa cuando se tiene información sobre el ángulo agudo y el cateto adyacente. En topografía y construcción, asimismo, se hacen mediciones relacionadas a estructuras de apoyo, pendientes y rampas.
Sirve, además, para solucionar o simplificar ecuaciones trigonométricas que poseen sec θ y resolver integrales que incluyen raíces cuadradas. También es interesante considerar que en el cálculo de velocidades angulares entra en juego la derivada de sec θ y que la secante aparece, incluso, en coordenadas polares.


 Publicado por
Publicado por