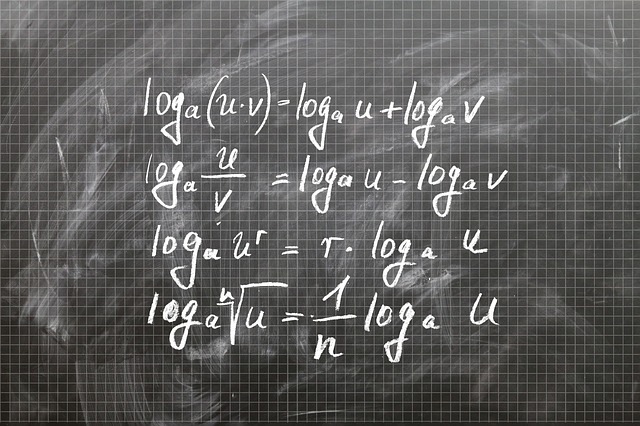
Un logaritmo es un exponente al cual se debe elevar una cantidad positiva para la obtención de un determinado número como resultado.
La etimología de logaritmo nos lleva a dos vocablos griegos: lógos (que se traduce como “razón”) y arithmós (traducible como “número”). El concepto se emplea en el terreno de las matemáticas.
Un logaritmo es el exponente al cual se necesita elevar una cantidad positiva para obtener como resultado un cierto número. Cabe recordar que un exponente, en tanto, es el número que denota la potencia a la cual debe elevarse otra cifra.
De este modo, el logaritmo de un número es el exponente al cual tiene que elevarse la base para llegar a dicho número. Muchas veces un cálculo aritmético puede realizarse de manera más simple apelando a los logaritmos.
 Temas
TemasEjemplo de logaritmo
Veamos un ejemplo. El logaritmo en base 5 de 625 es 4, ya que 625 es igual a 5 a la potencia 4: 5 x 5 x 5 x 5 = 625.
Dado un número (el argumento), la función logaritmo se encarga de asignarle un exponente (la potencia) al cual otro número fijo (la base) debe elevarse para obtener el argumento. Retomando nuestro ejemplo, el argumento es 625, la potencia es 4 y la base es 5.
Base a la potencia = Argumento
5 elevado a la 4 = 625
5 x 5 x 5 x 5 = 625

Los logaritmos se estudian en las matemáticas.
Los aportes de Napier y Euler
El escocés John Napier es señalado como el pionero en definir los logaritmos en el siglo XVII. Años más tarde, el suizo Leonhard Euler los vinculó con la función exponencial.
Con el objetivo de facilitar operaciones, los ingenieros y científicos de distintos ámbitos recurren cotidianamente a los logaritmos.
Logaritmo de una cantidad física y escala de medición
Se llama escala logarítmica, por otra parte, a la escala de medición que usa el logaritmo de una cantidad física en reemplazo de la cantidad en cuestión.
El concepto de escala de medición también se conoce como nivel de medida y se trata de una variable que sirve para describir la naturaleza de los datos que contienen los números que se asignan a los objetos y, por ende, los que contiene una variable.
Con respecto a cantidad física, significa una que pueda ser medida en el contexto de un sistema físico, o sea, a la cual es posible asignarle diferentes valores que partan de una medición.
A pesar de que el nombre pueda parecer poco común, todos hemos usado la escala logarítmica en la escuela incluso sin saberlo. Por ejemplo, se puede apreciar en las divisiones de los ejes cartesianos que se separan por distancias iguales tales como: 1, 10, 100, 1000, en lugar de 1, 2, 3, etcétera. Esto puede resultar ideal para graficar datos que se expandan a lo largo de una gama de valores considerable, ya que el rango se vuelve mucho más fácil de manipular.
Las bases de logaritmos que más se usan son el número e, base de los logaritmos neperianos o naturales, y 10, la de los decimales.
El vínculo entre los estímulos físicos y su magnitud
Gracias a los estudios científicos de personas como Ernst Heinrich Weber y Gustav Theodor Fechner, de finales del siglo XVIII y principios del XIX, respectivamente, sabemos que existe una relación cuantitativa entre la forma en la que percibimos los estímulos físicos y su magnitud. Esta teoría fue propuesta en el año 1860 y, en otras palabras, puede expresarse como que ciertos sentidos del ser humano trabajan de forma logarítmica.
Esto puede ayudarnos a entender algunas de las ventajas de usar escalas logarítmicas a la hora de representar ciertos valores, ya que nuestro cerebro entiende el concepto de logaritmo de una forma mucho más natural de lo que creemos. El oído, por ejemplo, es capaz de percibir diferencias iguales en la altura de los sonidos cuando recibe el estímulo de cocientes iguales de frecuencias.
Como si esto fuera poco, algunos estudios realizados en grupos de niños pequeños y en adultos de tribus alejadas de las grandes ciudades han probado que los seres humanos hacemos uso de las escalas logarítmicas de manera natural para representar los valores numéricos.

