
Una razón matemática expresa una proporción entre dos magnitudes.
La razón matemática es un vínculo entre dos magnitudes que son comparables entre sí. Se trata de aquello que resulta cuando una de las magnitudes o cantidades se divide o se resta por otra. Las razones, por lo tanto, pueden expresarse como fracciones o como números decimales.
Cabe destacar que razón es una noción con una gran cantidad de acepciones. En este caso nos interesa resaltar su uso en el ámbito de la matemática, donde la razón es el cociente de dos cifras.
 Temas
Temas Resumen
ResumenEjemplos de razón matemática
Veamos un ejemplo. La razón de 24 entre 6 es igual a 4. Esto quiere decir que si dividimos 24 en 6, obtendremos 4 como razón matemática.
24 / 6 = 4 (o, dicho de otro modo: 6 x 4 = 24).
Podemos afirmar, siguiendo con el mismo ejemplo, que 24 tiene 4 veces 6. También la razón puede expresarse como una fracción: en este caso, aquella que tiene al 24 como numerador y al 6 como denominador.
Otro ejemplo: 50 / 10 = 5. En este caso, la razón de 50 entre 10 equivale a 5. Como se puede advertir, 5 es el resultado de la división de 50 en 10 (y, por consiguiente, de multiplicar 10 por 5). Llevando estos cálculos a una situación cotidiana, si se reparten 50 golosinas entre 10 niños, cada pequeño recibirá 5 dulces.
La razón matemática revela la equivalencia que hay entre distintas cantidades.
El concepto en la geometría y la aritmética
Cabe destacar que, en muchas oportunidades, se distingue entre razón geométrica y razón aritmética. La razón geométrica supone el cociente de una progresión geométrica y consiste en comparar, como hicimos en los ejemplos anteriores, dos cantidades a partir de su cociente (determinando qué número de veces está presente una en la otra).
Dado que la razón geométrica se enmarca en el concepto de progresión geométrica, es necesario explicar también su significado: se trata de una secuencia en la cual cada elemento puede obtenerse a través de la multiplicación del anterior por una razón (una constante que también se conoce con el nombre de factor de la progresión). Por lo general, se prefiere el uso de la palabra progresión para aquellas secuencias que tienen un comienzo y un final bien definidos, mientras que sucesión se suele usar para los casos de términos infinitos.
Una progresión geométrica podría ser la siguiente: 4, 12, 36, 108, 324. En este caso, la razón matemática (o razón geométrica, para ser más precisos) es 3, ya que se trata del número por el cual es necesario multiplicar cada elemento para obtener el siguiente. La ecuación para poder acceder rápidamente a cualquier elemento de esta progresión tiene de un lado la incógnita con el número de orden (n) que deseamos averiguar como subíndice y del otro lado, el primero de los términos multiplicado por la razón elevada a la n menos 1.
Tomemos un ejemplo basado en la progresión geométrica anterior, para comprobar la efectividad de dicha ecuación a la hora de buscar el valor de cualquiera de sus elementos: si consideramos que 4 es el primero, el valor del quinto podemos averiguarlo multiplicando 4 por 3 (la razón matemática de esta progresión) elevado a la 4 (o sea, al número de orden del elemento que deseamos conocer, 5, menos 1); 3 elevado a la 4 nos da 81, que multiplicado por 4 nos devuelve 324.
A través de la comparación de razones matemáticas se puede saber si éstas son iguales o si hay una menor y otra mayor.
La razón aritmética, otro tipo de razón matemática
La razón aritmética, en cambio, es la diferencia que existe en una progresión aritmética. En este caso, la razón matemática es la diferencia entre ambas cifras (o sea, el resultado de la resta). La razón 8-3, en este sentido, es 5.
Una progresión aritmética, a diferencia de una geométrica, sirve para describir una sucesión numérica en la cual cada par de términos sucesivos tiene la misma diferencia que cualquier otro, ya que para obtener uno se debe sumar una constante al anterior. Dicha constante se conoce con el nombre de diferencia de la progresión o distancia. Tomando el ejemplo del párrafo anterior, si la razón matemática es 5, una posible progresión podría ser 3, 8, 13, 18 y 23.
Tanto en la razón geométrica como en la razón aritmética, en definitiva, se trabaja con la relación entre dos términos que son sucesivos, conocidos como antecedente y consecuente.
La noción en la trigonometría
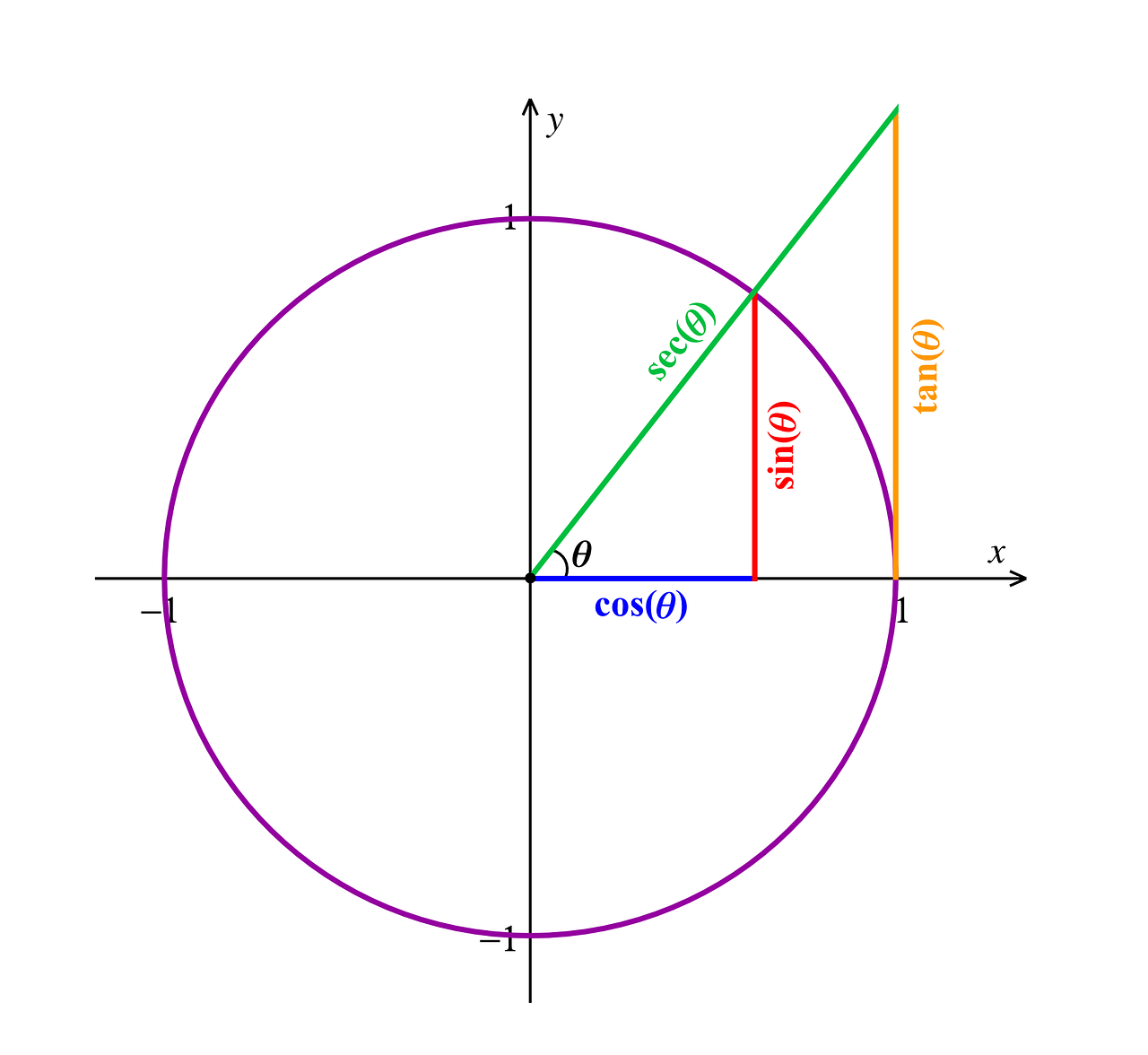
La trigonometría (área de las matemáticas vinculada a la medición de los triángulos) también apela a la razón entre magnitudes. Existen tres razones trigonométricas, cada una con su inversa correspondiente.
La tangente es una razón trigonométrica que relaciona el cateto opuesto al ángulo con el cateto adyacente. El seno, en tanto, es la razón del cateto que está opuesto al ángulo y la hipotenusa, mientras que el coseno es la razón entre el cateto que es adyacente al ángulo y la hipotenusa.
En cuanto a las relaciones inversas, se trata de la cotangente, la cosecante y la secante, asociadas a la tangente, el seno y el coseno, respectivamente.
Estas razones matemáticas que emplea la trigonometría suelen ser utilizadas para la medición de distancias. Los sistemas de navegación satelital (GPS), por ejemplo, recurren a ellas. Lo mismo hacen los astrónomos cuando desean calcular qué tan cerca o lejos se encuentran entre sí aquellas estrellas que se ubican en una misma zona.

